A graph can exist in different forms having the same number of vertices, edges, and also the same edge connectivity. Such graphs are called isomorphic graphs. Note that we label the graphs in this chapter mainly for the purpose of referring to them and recognizing them from one another.
Isomorphic Graphs
Two graphs G1 and G2 are said to be isomorphic if −
- Their number of components (vertices and edges) are same.
- Their edge connectivity is retained.
Note − In short, out of the two isomorphic graphs, one is a tweaked version of the other. An unlabelled graph also can be thought of as an isomorphic graph.
There exists a function ‘f’ from vertices of G1 to vertices of G2
[f: V(G1) ⇒ V(G2)], such that
Case (i): f is a bijection (both one-one and onto)
Case (ii): f preserves adjacency of vertices, i.e., if the edge {U, V} ∈ G1, then the
edge {f(U), f(V)} ∈ G2, then G1 ≡ G2.
Note
If G1 ≡ G2 then −
· |V(G1)| = |V(G2)|
· |E(G1)| = |E(G2)|
· Degree sequences of G1 and G2 are same.
· If the vertices {V1, V2, .. Vk} form a cycle of length K in G1, then the vertices {f(V1), f(V2),… f(Vk)} should form a cycle of length K in G2.
All the above conditions are necessary for the graphs G1 and G2 to be isomorphic, but not sufficient to prove that the graphs are isomorphic.
· (G1 ≡ G2) if and only if (G1− ≡ G2−) where G1 and G2 are simple graphs.
· (G1 ≡ G2) if the adjacency matrices of G1 and G2 are same.
· (G1 ≡ G2) if and only if the corresponding subgraphs of G1 and G2 (obtained by deleting some vertices in G1 and their images in graph G2) are isomorphic.
Example
Which of the following graphs are isomorphic?
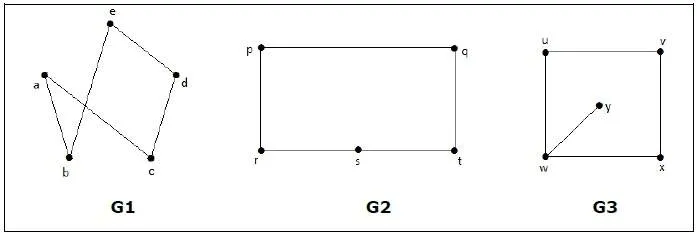
In the graph G3, vertex ‘w’ has only degree 3, whereas all the other graph vertices has degree 2. Hence G3 not isomorphic to G1 or G2.
Taking complements of G1 and G2, you have −
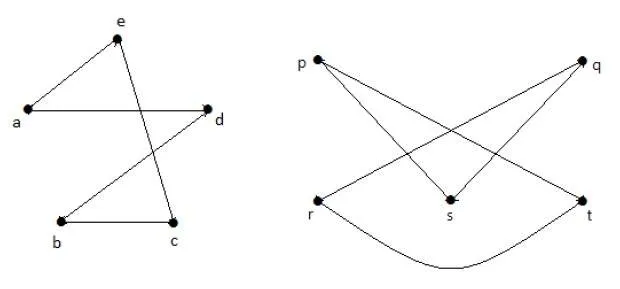
Here, (G1− ≡ G2−), hence (G1 ≡ G2).
Planar Graphs
A graph ‘G’ is said to be planar if it can be drawn on a plane or a sphere so that no two edges cross each other at a non-vertex point.
Example
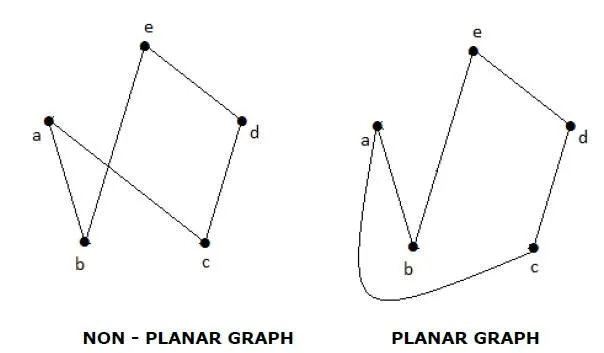
Regions
Every planar graph divides the plane into connected areas called regions.
Example
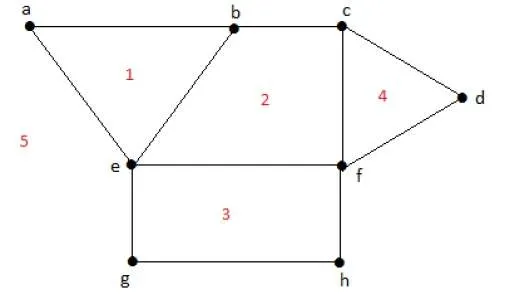
Degree of a bounded region r = deg(r) = Number of edges enclosing the regions r.
deg(1) = 3
deg(2) = 4
deg(3) = 4
deg(4) = 3
deg(5) = 8
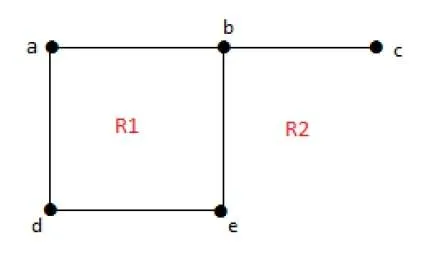
Degree of an unbounded region r = deg(r) = Number of edges enclosing the regions r.
deg(R1) = 4
deg(R2) = 6
In planar graphs, the following properties hold good −
· 1. In a planar graph with ‘n’ vertices, sum of degrees of all the vertices is
n ∑ i=1 deg(Vi) = 2|E|
· 2. According to Sum of Degrees of Regions Theorem, in a planar graph with ‘n’ regions, Sum of degrees of regions is −
n ∑ i=1 deg(ri) = 2|E|
Based on the above theorem, you can draw the following conclusions −
In a planar graph,
· If degree of each region is K, then the sum of degrees of regions is
K|R| = 2|E|
· If the degree of each region is at least K(≥ K), then
K|R| ≤ 2|E|
· If the degree of each region is at most K(≤ K), then
K|R| ≥ 2|E|
Note − Assume that all the regions have same degree.
3. According to Euler’s Formulae on planar graphs,
· If a graph ‘G’ is a connected planar, then
|V| + |R| = |E| + 2
· If a planar graph with ‘K’ components then
|V| + |R|=|E| + (K+1)
Where, |V| is the number of vertices, |E| is the number of edges, and |R| is the number of regions.
4. Edge Vertex Inequality
If ‘G’ is a connected planar graph with degree of each region at least ‘K’ then,
|E| ≤ kk − 2{|v| – 2}
You know, |V| + |R| = |E| + 2
K.|R| ≤ 2|E|
K(|E| – |V| + 2) ≤ 2|E|
(K – 2)|E| ≤ K(|V| – 2)
|E| ≤ kk − 2{|v| – 2}
5. If ‘G’ is a simple connected planar graph, then
|E| ≤ 3|V| − 6
|R| ≤ 2|V| − 4
There exists at least one vertex V ∈ G, such that deg(V) ≤ 5
6. If ‘G’ is a simple connected planar graph (with at least 2 edges) and no triangles, then
|E| ≤ {2|V| – 4}
7. Kuratowski’s Theorem
A graph ‘G’ is non-planar if and only if ‘G’ has a subgraph which is homeomorphic to K5 or K3,3.
Homomorphism
Two graphs G1 and G2 are said to be homomorphic, if each of these graphs can be obtained from the same graph ‘G’ by dividing some edges of G with more vertices. Take a look at the following example −
Divide the edge ‘rs’ into two edges by adding one vertex.
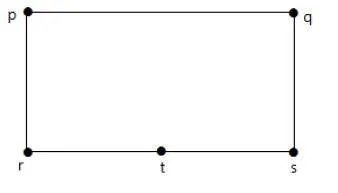
The graphs shown below are homomorphic to the first graph.
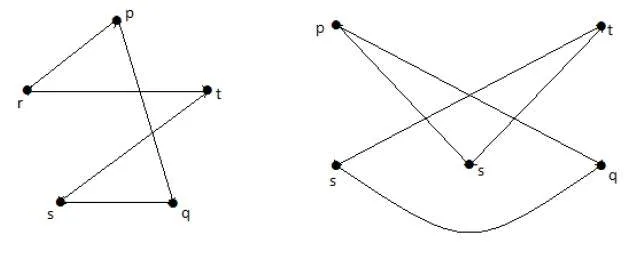
If G1 is isomorphic to G2, then G is homeomorphic to G2 but the converse need not be true.
· Any graph with 4 or less vertices is planar.
· Any graph with 8 or less edges is planar.
· A complete graph Kn is planar if and only if n ≤ 4.
· The complete bipartite graph Km, n is planar if and only if m ≤ 2 or n ≤ 2.
· A simple non-planar graph with minimum number of vertices is the complete graph K5.
· The simple non-planar graph with minimum number of edges is K3, 3.
Polyhedral graph
A simple connected planar graph is called a polyhedral graph if the degree of each vertex is ≥ 3, i.e., deg(V) ≥ 3 ∀ V ∈ G.
- 3|V| ≤ 2|E|
- 3|R| ≤ 2|E|
