Walks
| Definition: For a graph G=(V(G),E(G)), a Walk is defined as a sequence of alternating vertices and edges such as v0,e1,v1,e2,…,ek,vk where each edge ei={vi−1,vi}. The Length of this walk is k. |
For example, the graph below outlines a possibly walk (in blue). The walk is denoted as abcdb. Note that walks can have repeated edges. For example, if we had the walk abcdcbce, then that would be perfectly fine even though some edges are repeated.
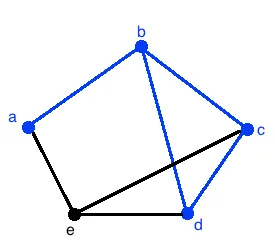
Note that the length of a walk is simply the number of edges passed in that walk. In the graph above, the length of the walk is abcdb is 4 because it passes through 4 edges.
Open / Closed Walks
| Definition: A walk is considered to be Closed if the starting vertex is the same as the ending vertex, that is v0=vk. A walk is considered Open otherwise. |
For example, the follow graph shows a closed walk in green:
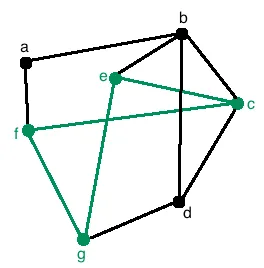
Notice that the walk can be defined by cegfc, and the start and end vertices of the walk is c. Hence this walk is closed.
Trails
| Definition: A Trail is defined as a walk with no repeated edges. |
So far, both of the earlier examples can be considered trails because there are no repeated edges. Here is another example of a trail:
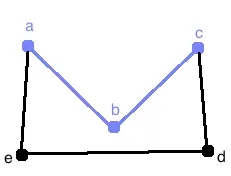
Notice that the walk can be defined as abc. There are no repeated edges so this walk is also a trail.
Now let’s look at the next graph:
Notice that this walk must repeat at least one edge.
Paths
| Definition: A Path is defined as an open trail with no repeated vertices. |
Notice that all paths must therefore be open walks, as a path cannot both start and terminate at the same vertex. For example, the following orange coloured walk is a path
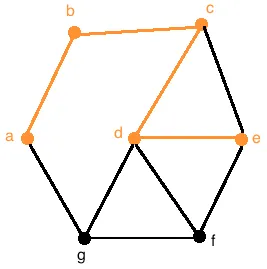
because the walk abcde does not repeat any edges.
Now let’s look at the next graph with the teal walk. This walk is NOT a path since it repeats a vertex, namely the pink vertex c:
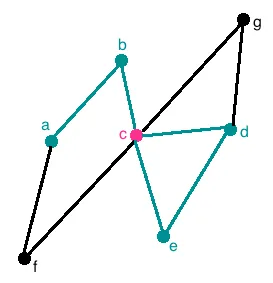
Cycles
| Definition: A Cycle is defined as a closed trail where no other vertices are repeated apart from the start/end vertex. |
Below is an example of a circuit. Notice how no edges are repeated in the walk bcgfb, which makes it definitely a trail, and that the start and end vertex b is the same which makes it closed.
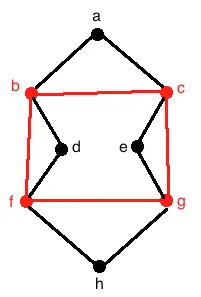
Circuits
| Definition: A Circuit is a closed trail. That is, a circuit has no repeated edges but may have repeated vertices. |
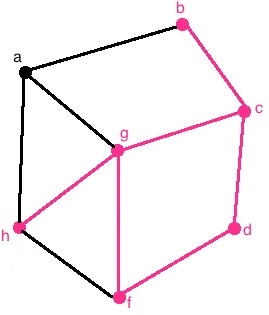
An example of a circuit can be seen below. Notice how there are no edges repeated in the walk hbcdefcgh, hence the walk is certainly a trail. Additionally, the trail is closed, hence it is by definition a circuit.
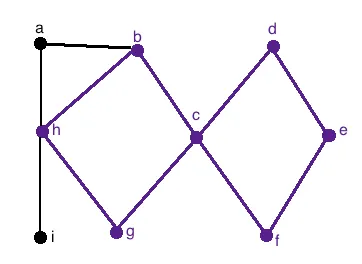

Comments are closed.