Suppose we have to encode a text that comprises symbols from some n-symbol alphabet by assigning to each of the text’s symbols some sequence of bits called the codeword. For example, we can use a fixed-length encoding that assigns to each symbol a bit string of the same length m (m ≥ log2 n). This is exactly what the standard ASCII code does. One way of getting a coding scheme that yields a shorter bit string on the average is based on the old idea of assigning shorter code-words to more frequent symbols and longer codewords to less frequent symbols. This idea was used, in particular, in the telegraph code invented in the mid-19th century by Samuel Morse. In that code, frequent letters such as e (.) and a (.−) are assigned short sequences of dots and dashes while infrequent letters such as q (− − .−) and z (− − ..) have longer ones.
Variable-length encoding, which assigns codewords of different lengths todifferent symbols, introduces a problem that fixed-length encoding does not have. Namely, how can we tell how many bits of an encoded text represent the first (or, more generally, the ith) symbol? To avoid this complication, we can limit ourselves to the so-called prefix-free (or simply prefix) codes. In a prefix code, no codeword is a prefix of a codeword of another symbol. Hence, with such an encoding, we can simply scan a bit string until we get the first group of bits that is a codeword for some symbol, replace these bits by this symbol, and repeat this operation until the bit string’s end is reached.
If we want to create a binary prefix code for some alphabet, it is natural to associate the alphabet’s symbols with leaves of a binary tree in which all the left edges are labeled by 0 and all the right edges are labeled by 1. The codeword of a symbol can then be obtained by recording the labels on the simple path from the root to the symbol’s leaf. Since there is no simple path to a leaf that continues to another leaf, no codeword can be a prefix of another codeword; hence, any such tree yields a prefix code.
Among the many trees that can be constructed in this manner for a given alphabet with known frequencies of the symbol occurrences, how can we construct a tree that would assign shorter bit strings to high-frequency symbols and longer ones to low-frequency symbols? It can be done by the following greedy algorithm, invented by David Huffman while he was a graduate student at MIT [Huf52].
Huffman’s algorithm
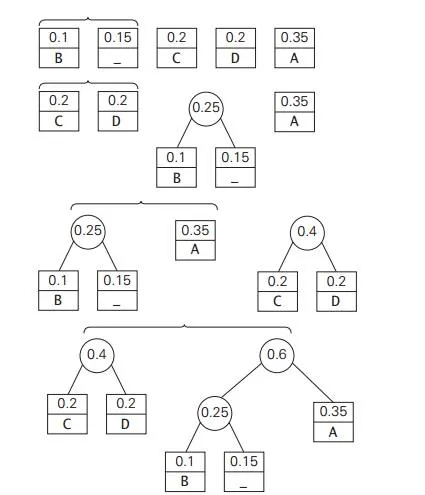
Step 1 Initializen one-node trees and label them with the symbols of thealphabet given. Record the frequency of each symbol in its tree’s root to indicate the tree’s weight. (More generally, the weight of a tree will be equal to the sum of the frequencies in the tree’s leaves.)
Step 2 Repeat the following operation until a single tree is obtained. Findtwo trees with the smallest weight (ties can be broken arbitrarily, but see Problem 2 in this section’s exercises). Make them the left and right subtree of a new tree and record the sum of their weights in the root of the new tree as its weight.
A tree constructed by the above algorithm is called a Huffman tree. It defines—in the manner described above—a Huffman code.
EXAMPLE Consider the five-symbol alphabet {A, B, C, D, _}with the following occurrence frequencies in a text made up of these symbols:

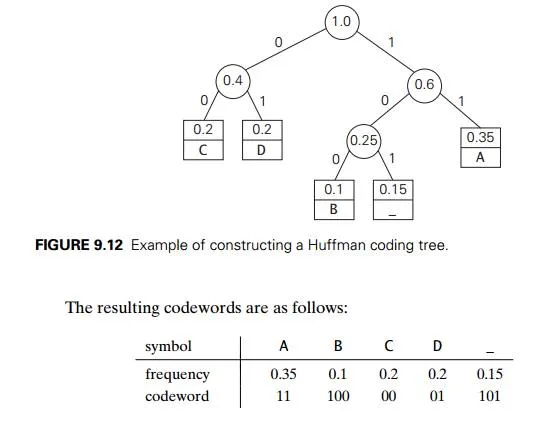
Hence, DAD is encoded as 011101, and 10011011011101 is decoded as BAD_AD. With the occurrence frequencies given and the codeword lengths obtained,
the average number of bits per symbol in this code is
2 . 0.35 + 3 . 0.1 + 2 . 0.2 + 2 . 0.2 + 3 . 0.15 = 2.25.
Had we used a fixed-length encoding for the same alphabet, we would have to use at least 3 bits per each symbol. Thus, for this toy example, Huffman’s code achieves the compression ratio—a standard measure of a compression algorithm’s effectiveness—of (3 − 2.25)/3 . 100% = 25%. In other words, Huffman’s encoding of the text will use 25% less memory than its fixed-length encoding. (Extensive experiments with Huffman codes have shown that the compression ratio for this scheme typically falls between 20% and 80%, depending on the characteristics of the text being compressed.)
Huffman’s encoding is one of the most important file-compression methods. In addition to its simplicity and versatility, it yields an optimal, i.e., minimal-length, encoding (provided the frequencies of symbol occurrences are independent and known in advance). The simplest version of Huffman compression calls, in fact, for a preliminary scanning of a given text to count the frequencies of symbol occurrences in it. Then these frequencies are used to construct a Huffman coding tree and encode the text as described above. This scheme makes it necessary, however, to include the coding table into the encoded text to make its decoding possible. This drawback can be overcome by using dynamic Huffman encoding, in which the coding tree is updated each time a new symbol is read from the source text. Further, modern alternatives such as Lempel-Ziv algorithms (e.g., [Say05]) assign codewords not to individual symbols but to strings of symbols, allowing them to achieve better and more robust compressions in many applications.
It is important to note that applications of Huffman’s algorithm are not limited to data compression. Suppose we have n positive numbers w1, w2, . . . , wn that have to be assigned to n leaves of a binary tree, one per node. If we define the
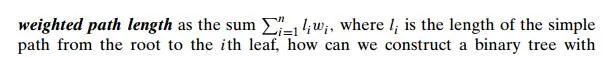
minimum weighted path length? It is this more general problem that Huffman’s algorithm actually solves. (For the coding application, li and wi are the length of the codeword and the frequency of the ith symbol, respectively.)
This problem arises in many situations involving decision making. Consider, for example, the game of guessing a chosen object from n possibilities (say, an integer between 1 and n) by asking questions answerable by yes or no. Different strategies for playing this game can be modeled by decision trees5 such as those depicted in Figure 9.13 for n = 4. The length of the simple path from the root to a leaf in such a tree is equal to the number of questions needed to get to the chosen number represented by the leaf. If number i is chosen with probability pi, the sum
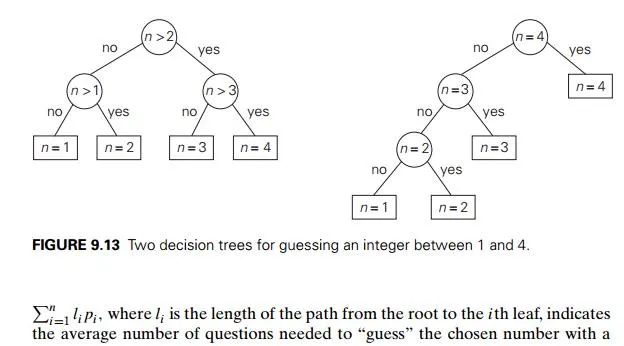
the average number of questions needed to “guess” the chosen number with a game strategy represented by its decision tree. If each of the numbers is chosen with the same probability of 1/n, the best strategy is to successively eliminate half (or almost half) the candidates as binary search does. This may not be the case for arbitrary pi’s, however. For example, if n = 4 and p1 = 0.1, p2 = 0.2, p3 = 0.3, and p4 = 0.4, the minimum weighted path tree is the rightmost one in Figure 9.13. Thus, we need Huffman’s algorithm to solve this problem in its general case.
Note that this is the second time we are encountering the problem of con-structing an optimal binary tree. In Section 8.3, we discussed the problem of constructing an optimal binary search tree with positive numbers (the search prob-abilities) assigned to every node of the tree. In this section, given numbers are assigned just to leaves. The latter problem turns out to be easier: it can be solved by the greedy algorithm, whereas the former is solved by the more complicated dynamic programming algorithm.
Exercises 9.4
1. a. Construct a Huffman code for the following data:

Encode ABACABAD using the code of question (a).
Decode 100010111001010 using the code of question (a).
For data transmission purposes, it is often desirable to have a code with a minimum variance of the codeword lengths (among codes of the same average length). Compute the average and variance of the codeword length in two
Huffman codes that result from a different tie breaking during a Huffman code construction for the following data:

Indicate whether each of the following properties is true for every Huffman code.
The codewords of the two least frequent symbols have the same length.
The codeword’s length of a more frequent symbol is always smaller than or equal to the codeword’s length of a less frequent one.
What is the maximal length of a codeword possible in a Huffman encoding of an alphabet of n symbols?
a. Write pseudocode of the Huffman-tree construction algorithm.
What is the time efficiency class of the algorithm for constructing a Huff-man tree as a function of the alphabet size?
Show that a Huffman tree can be constructed in linear time if the alphabet symbols are given in a sorted order of their frequencies.
Given a Huffman coding tree, which algorithm would you use to get the codewords for all the symbols? What is its time-efficiency class as a function of the alphabet size?
Explain how one can generate a Huffman code without an explicit generation of a Huffman coding tree.
a. Write a program that constructs a Huffman code for a given English textand encode it.
Write a program for decoding of an English text which has been encoded with a Huffman code.
Experiment with your encoding program to find a range of typical compres-sion ratios for Huffman’s encoding of English texts of, say, 1000 words.
Experiment with your encoding program to find out how sensitive the compression ratios are to using standard estimates of frequencies instead of actual frequencies of symbol occurrences in English texts.
Card guessing Design a strategy that minimizes the expected number ofquestions asked in the following game [Gar94]. You have a deck of cards that consists of one ace of spades, two deuces of spades, three threes, and on up to nine nines, making 45 cards in all. Someone draws a card from the shuffled deck, which you have to identify by asking questions answerable with yes or no.


Comments are closed.