In the previous section, we considered the greedy algorithm that “grows” a mini-mum spanning tree through a greedy inclusion of the nearest vertex to the vertices already in the tree. Remarkably, there is another greedy algorithm for the mini-mum spanning tree problem that also always yields an optimal solution. It is named Kruskal’s algorithm after Joseph Kruskal, who discovered this algorithm whenhe was a second-year graduate student [Kru56]. Kruskal’s algorithm looks at a minimum spanning tree of a weighted connected graph G = V , E as an acyclic subgraph with |V | − 1 edges for which the sum of the edge weights is the smallest. (It is not difficult to prove that such a subgraph must be a tree.) Consequently, the algorithm constructs a minimum spanning tree as an expanding sequence of subgraphs that are always acyclic but are not necessarily connected on the inter-mediate stages of the algorithm.
The algorithm begins by sorting the graph’s edges in nondecreasing order of their weights. Then, starting with the empty subgraph, it scans this sorted list, adding the next edge on the list to the current subgraph if such an inclusion does not create a cycle and simply skipping the edge otherwise.
ALGORITHM Kruskal(G)
//Kruskal’s algorithm for constructing a minimum spanning tree //Input: A weighted connected graph G = V , E
//Output: ET , the set of edges composing a minimum spanning tree of G sort E in nondecreasing order of the edge weights w(ei1) ≤ . . . ≤ w(ei|E| )

The correctness of Kruskal’s algorithm can be proved by repeating the essen-tial steps of the proof of Prim’s algorithm given in the previous section. The fact that ET is actually a tree in Prim’s algorithm but generally just an acyclic subgraph in Kruskal’s algorithm turns out to be an obstacle that can be overcome.
Figure 9.5 demonstrates the application of Kruskal’s algorithm to the same graph we used for illustrating Prim’s algorithm in Section 9.1. As you trace the algorithm’s operations, note the disconnectedness of some of the intermediate subgraphs.
Applying Prim’s and Kruskal’s algorithms to the same small graph by hand may create the impression that the latter is simpler than the former. This impres-sion is wrong because, on each of its iterations, Kruskal’s algorithm has to check whether the addition of the next edge to the edges already selected would create a
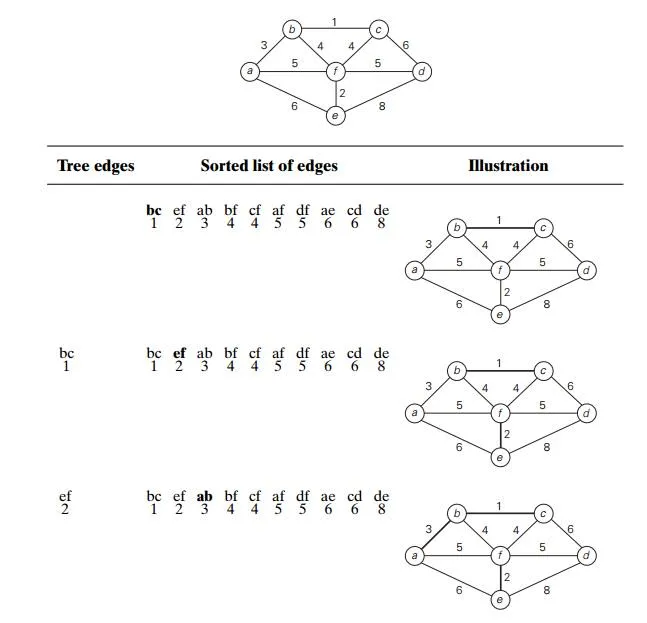
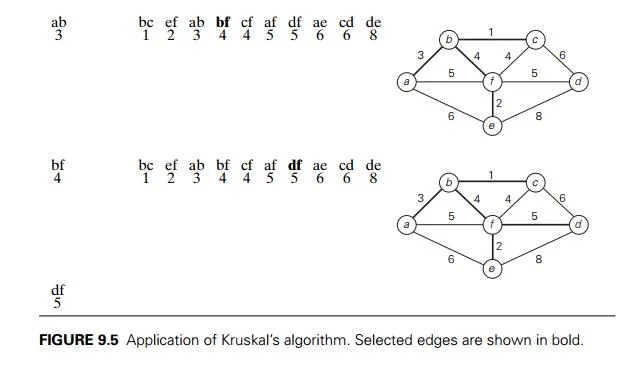
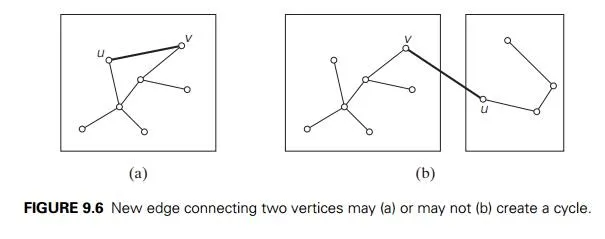
cycle. It is not difficult to see that a new cycle is created if and only if the new edge connects two vertices already connected by a path, i.e., if and only if the two ver-tices belong to the same connected component (Figure 9.6). Note also that each connected component of a subgraph generated by Kruskal’s algorithm is a tree because it has no cycles.
In view of these observations, it is convenient to use a slightly different interpretation of Kruskal’s algorithm. We can consider the algorithm’s operations as a progression through a series of forests containing all the vertices of a given graph and some of its edges. The initial forest consists of |V | trivial trees, each comprising a single vertex of the graph. The final forest consists of a single tree, which is a minimum spanning tree of the graph. On each iteration, the algorithm takes the next edge (u, v) from the sorted list of the graph’s edges, finds the trees containing the vertices u and v, and, if these trees are not the same, unites them in a larger tree by adding the edge (u, v).
Fortunately, there are efficient algorithms for doing so, including the crucial check for whether two vertices belong to the same tree. They are called union-find algorithms. We discuss them in the following subsection. With an efficientunion-find algorithm, the running time of Kruskal’s algorithm will be dominated by the time needed for sorting the edge weights of a given graph. Hence, with an efficient sorting algorithm, the time efficiency of Kruskal’s algorithm will be in
O(|E|log |E|).
Disjoint Subsets and Union-Find Algorithms
Kruskal’s algorithm is one of a number of applications that require a dynamic partition of some n element set S into a collection of disjoint subsets S1, S2, . . . , Sk. After being initialized as a collection of n one-element subsets, each containing a different element of S, the collection is subjected to a sequence of intermixed union and find operations. (Note that the number of union operations in any such sequence must be bounded above by n − 1 because each union increases a subset’s size at least by 1 and there are only n elements in the entire set S.) Thus, we are dealing here with an abstract data type of a collection of disjoint subsets of a finite set with the following operations:
makeset(x) creates a one-element set{x}. It is assumed that this operation canbe applied to each of the elements of set S only once.
find(x) returns a subset containingx.
union(x, y) constructs the union of the disjoint subsetsSx andSy containingx and y, respectively, and adds it to the collection to replace Sx and Sy, which are deleted from it.
For example, let S = {1, 2, 3, 4, 5, 6}. Then makeset(i) creates the set {i} and applying this operation six times initializes the structure to the collection of six singleton sets:
{1}, {2}, {3}, {4}, {5}, {6}.
Performing union(1, 4) and union(5, 2) yields
{1, 4}, {5, 2}, {3}, {6},
and, if followed by union(4, 5) and then by union(3, 6), we end up with the disjoint subsets
{1, 4, 5, 2}, {3, 6}.
Most implementations of this abstract data type use one element from each of the disjoint subsets in a collection as that subset’s representative. Some implemen-tations do not impose any specific constraints on such a representative; others do so by requiring, say, the smallest element of each subset to be used as the subset’s representative. Also, it is usually assumed that set elements are (or can be mapped into) integers.
There are two principal alternatives for implementing this data structure. The first one, called the quick find, optimizes the time efficiency of the find operation; the second one, called the quick union, optimizes the union operation.
The quick find uses an array indexed by the elements of the underlying set S; the array’s values indicate the representatives of the subsets containing those elements. Each subset is implemented as a linked list whose header contains the pointers to the first and last elements of the list along with the number of elements in the list (see Figure 9.7 for an example).
Under this scheme, the implementation of makeset(x) requires assigning the corresponding element in the representative array to x and initializing the corre-sponding linked list to a single node with the x value. The time efficiency of this operation is obviously in (1), and hence the initialization of n singleton subsets is in (n). The efficiency of find(x) is also in (1): all we need to do is to retrieve the x’s representative in the representative array. Executing union(x, y) takes longer. A straightforward solution would simply append the y’s list to the end of the x’s list, update the information about their representative for all the elements in the

y list, and then delete the y’s list from the collection. It is easy to verify, however, that with this algorithm the sequence of union operations
union(2, 1), union(3, 2), . . . , union(i + 1, i), . . . , union(n, n − 1)
runs in (n2) time, which is slow compared with several known alternatives.
A simple way to improve the overall efficiency of a sequence of union oper-ations is to always append the shorter of the two lists to the longer one, with ties broken arbitrarily. Of course, the size of each list is assumed to be available by, say, storing the number of elements in the list’s header. This modification is called the
union by size. Though it does not improve the worst-case efficiency of a single ap-plication of the union operation (it is still in (n)), the worst-case running time of any legitimate sequence of union-by-size operations turns out to be in O(n log n).3 Here is a proof of this assertion. Let ai be an element of set S whose disjoint subsets we manipulate, and let Ai be the number of times ai’s representative is updated in a sequence of union-by-size operations. How large can Ai get if set S has n elements? Each time ai’s representative is updated, ai must be in a smaller subset involved in computing the union whose size will be at least twice as large as the size of the subset containing ai. Hence, when ai’s representative is updated for the first time, the resulting set will have at least two elements; when it is updated for the second time, the resulting set will have at least four elements; and, in general, if it is updated Ai times, the resulting set will have at least 2Ai elements. Since the entire set S has n elements, 2Ai ≤ n and hence Ai ≤ log2 n. Therefore, the total number of possible updates of the representatives for all n elements in S
will not exceed n log2 n.
Thus, for union by size, the time efficiency of a sequence of at most n − 1 unions and m finds is in O(n log n + m).
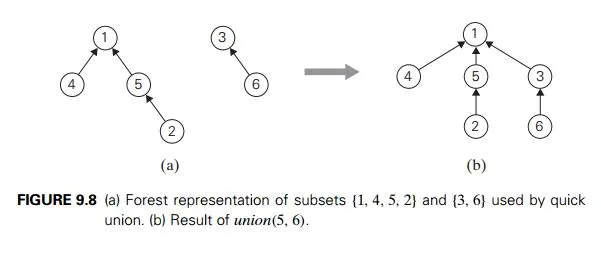
The quick union—the second principal alternative for implementing disjoint subsets—represents each subset by a rooted tree. The nodes of the tree contain the subset’s elements (one per node), with the root’s element considered the subset’s representative; the tree’s edges are directed from children to their parents (Figure 9.8). In addition, a mapping of the set elements to their tree nodes— implemented, say, as an array of pointers—is maintained. This mapping is not shown in Figure 9.8 for the sake of simplicity.
For this implementation, makeset(x) requires the creation of a single-node tree, which is a (1) operation; hence, the initialization of n singleton subsets is in (n). A union(x, y) is implemented by attaching the root of the y’s tree to the root of the x’s tree (and deleting the y’s tree from the collection by making the pointer to its root null). The time efficiency of this operation is clearly (1). A find(x) is
performed by following the pointer chain from the node containing x to the tree’s root whose element is returned as the subset’s representative. Accordingly, the time efficiency of a single find operation is in O(n) because a tree representing a subset can degenerate into a linked list with n nodes.
This time bound can be improved. The straightforward way for doing so is to always perform a union operation by attaching a smaller tree to the root of a larger one, with ties broken arbitrarily. The size of a tree can be measured either by the number of nodes (this version is called union by size) or by its height (this version is called union by rank). Of course, these options require storing, for each node of the tree, either the number of node descendants or the height of the subtree rooted at that node, respectively. One can easily prove that in either case the height of the tree will be logarithmic, making it possible to execute each find in O(log n) time. Thus, for quick union, the time efficiency of a sequence of at most n − 1 unions and m finds is in O(n + m log n).
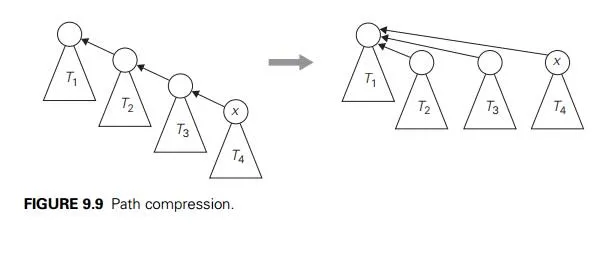
In fact, an even better efficiency can be obtained by combining either vari-ety of quick union with path compression. This modification makes every node encountered during the execution of a find operation point to the tree’s root (Fig-ure 9.9). According to a quite sophisticated analysis that goes beyond the level of this book (see [Tar84]), this and similar techniques improve the efficiency of a sequence of at most n − 1 unions and m finds to only slightly worse than linear.
Exercises 9.2
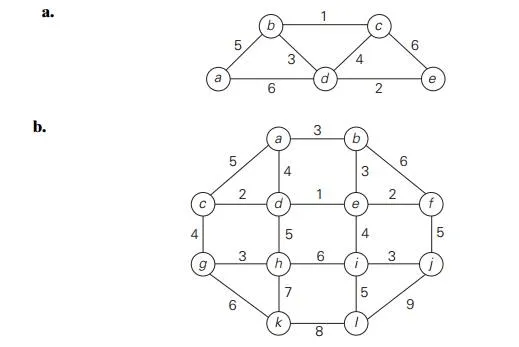
Apply Kruskal’s algorithm to find a minimum spanning tree of the following graphs.
Indicate whether the following statements are true or false:
If e is a minimum-weight edge in a connected weighted graph, it must be among edges of at least one minimum spanning tree of the graph.
If e is a minimum-weight edge in a connected weighted graph, it must be among edges of each minimum spanning tree of the graph.
If edge weights of a connected weighted graph are all distinct, the graph must have exactly one minimum spanning tree.
If edge weights of a connected weighted graph are not all distinct, the graph must have more than one minimum spanning tree.
What changes, if any, need to be made in algorithm Kruskal to make it find a minimum spanning forest for an arbitrary graph? (A minimum spanning forest is a forest whose trees are minimum spanning trees of the graph’s connected components.)
Does Kruskal’s algorithm work correctly on graphs that have negative edge weights?
Design an algorithm for finding a maximum spanning tree—a spanning tree with the largest possible edge weight—of a weighted connected graph.
Rewrite pseudocode of Kruskal’s algorithm in terms of the operations of the disjoint subsets’ ADT.
Prove the correctness of Kruskal’s algorithm.
Prove that the time efficiency of find(x) is in O(log n) for the union-by-size version of quick union.
Find at least two Web sites with animations of Kruskal’s and Prim’s algorithms. Discuss their merits and demerits.
Design and conduct an experiment to empirically compare the efficiencies of Prim’s and Kruskal’s algorithms on random graphs of different sizes and densities.
Steiner tree Four villages are located at the vertices of a unit square in theEuclidean plane. You are asked to connect them by the shortest network of roads so that there is a path between every pair of the villages along those roads. Find such a network.
Write a program generating a random maze based on
Prim’s algorithm.
Kruskal’s algorithm.


