In many situations we are faced with a problem of pairing elements of two sets. The traditional example is boys and girls for a dance, but you can easily think of more serious applications. It is convenient to represent elements of two given sets by vertices of a graph, with edges between vertices that can be paired. A matching in a graph is a subset of its edges with the property that no two edgesshare a vertex. A maximum matching—more precisely, a maximum cardinality matching—is a matching with the largest number of edges. (What is it for the graphin Figure 10.8? Is it unique?) The maximum-matching problem is the problem of finding a maximum matching in a given graph. For an arbitrary graph, this is a rather difficult problem. It was solved in 1965 by Jack Edmonds [Edm65]. (See [Gal86] for a good survey and more recent references.)
We limit our discussion in this section to the simpler case of bipartite graphs. In a bipartite graph, all the vertices can be partitioned into two disjoint sets V and U , not necessarily of the same size, so that every edge connects a vertex in one of these sets to a vertex in the other set. In other words, a graph is bipartite if its vertices can be colored in two colors so that every edge has its vertices colored in different colors; such graphs are also said to be 2-colorable. The graph in Figure 10.8 is bipartite. It is not difficult to prove that a graph is bipartite if and only if it does not have a cycle of an odd length. We will assume for the rest of this section that
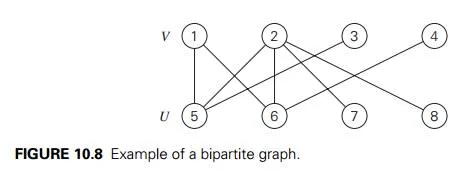
the vertex set of a given bipartite graph has been already partitioned into sets V and U as required by the definition (see Problem 8 in Exercises 3.5).
Let us apply the iterative-improvement technique to the maximum-cardinality-matching problem. Let M be a matching in a bipartite graph G = V , U, E . How can we improve it, i.e., find a new matching with more edges? Obviously, if every vertex in either V or U is matched (has a mate), i.e., serves as an endpoint of an edge in M, this cannot be done and M is a maximum matching. Therefore, to have a chance at improving the current matching, both V and U must contain unmatched (also called free) vertices, i.e., vertices that are not inci-dent to any edge in M. For example, for the matching Ma = {(4, 8), (5, 9)} in the graph in Figure 10.9a, vertices 1, 2, 3, 6, 7, and 10 are free, and vertices 4, 5, 8, and 9 are matched.
Another obvious observation is that we can immediately increase a current matching by adding an edge between two free vertices. For example, adding (1, 6) to the matching Ma = {(4, 8), (5, 9)} in the graph in Figure 10.9a yields a larger matching Mb = {(1, 6), (4, 8), (5, 9)} (Figure 10.9b). Let us now try to find a matching larger than Mb by matching vertex 2. The only way to do this would be to include the edge (2, 6) in a new matching. This inclusion requires removal of (1, 6), which can be compensated by inclusion of (1, 7) in the new matching. This new matching Mc = {(1, 7), (2, 6), (4, 8), (5, 9)} is shown in Figure 10.9c.
In general, we increase the size of a current matching M by constructing a simple path from a free vertex in V to a free vertex in U whose edges are alternately in E − M and in M. That is, the first edge of the path does not belong to M, the second one does, and so on, until the last edge that does not belong to M. Such a path is called augmenting with respect to the matching M. For example, the path 2, 6, 1, 7 is an augmenting path with respect to the matching Mb in Figure 10.9b. Since the length of an augmenting path is always odd, adding to the matching M the path’s edges in the odd-numbered positions and deleting from it the path’s edges in the even-numbered positions yields a matching with one more edge than in M. Such a matching adjustment is called augmentation. Thus, in Figure 10.9, the matching Mb was obtained by augmentation of the matching Ma along the augmenting path 1, 6, and the matching Mc was obtained by augmentation of the matching Mb along the augmenting path 2, 6, 1, 7. Moving further, 3, 8, 4, 9, 5, 10 is an augmenting path for the matching Mc (Figure 10.9c). After adding to Mc the edges (3, 8), (4, 9), and (5, 10) and deleting (4, 8) and (5, 9), we obtain the matching Md = {(1, 7), (2, 6), (3, 8), (4, 9), (5, 10)} shown in Figure 10.9d. The
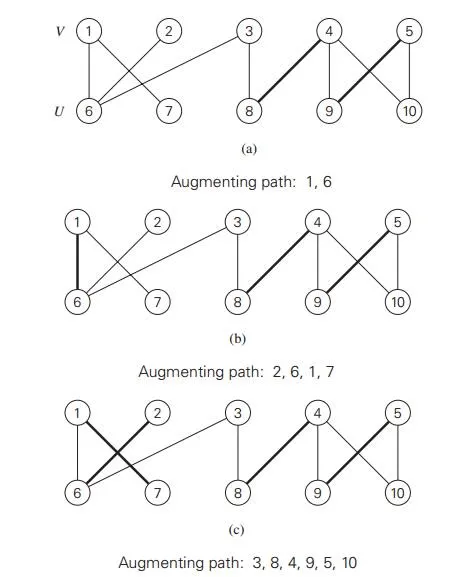
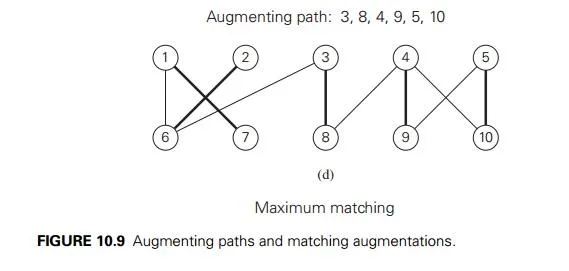
matching Md is not only a maximum matching but also perfect, i.e., a matching that matches all the vertices of the graph.
Before we discuss an algorithm for finding an augmenting path, let us settle the issue of what nonexistence of such a path means. According to the theorem discovered by the French mathematician Claude Berge, it means the current matching is maximal.
THEOREM A matching M is a maximum matching if and only if there exists no augmenting path with respect to M.
PROOF If an augmenting path with respect to a matching M exists, then the size of the matching can be increased by augmentation. Let us prove the more difficult part: if no augmenting path with respect to a matching M exists, then the matching is a maximum matching. Assume that, on the contrary, this is not the case for a certain matching M in a graph G. Let M∗ be a maximum matching in G; by our assumption, the number of edges in M∗ is at least one more than the number of edges in M, i.e., |M∗| > |M|. Consider the edges in the symmetric difference
⊕ M∗ = (M − M∗) ∪ (M∗ − M), the set of all the edges that are either in M or in M∗ but not in both. Note that |M∗ − M| > |M − M∗| because |M∗| > |M| by assumption. Let G be the subgraph of G made up of all the edges in M ⊕ M∗ and their endpoints. By definition of a matching, any vertex in G ⊆ G can be incident to no more than one edge in M and no more than one edge in M∗. Hence, each of the vertices in G has degree 2 or less, and therefore every connected component of G is either a path or an even-length cycle of alternating edges from M − M∗ and
∗ − M. Since |M∗ − M| > |M − M∗| and the number of edges from M − M∗ and
∗ − M is the same for any even-length cycle of alternating edges in G , there must exist at least one path of alternating edges that starts and ends with an edge from
∗ − M. Hence, this is an augmenting path for the matching M, which contradicts the assumption that no such path exists.
Our discussion of augmenting paths leads to the following general method for constructing a maximum matching in a bipartite graph. Start with some initial matching (e.g., the empty set). Find an augmenting path and augment the current matching along this path. When no augmenting path can be found, terminate the algorithm and return the last matching, which is maximum.
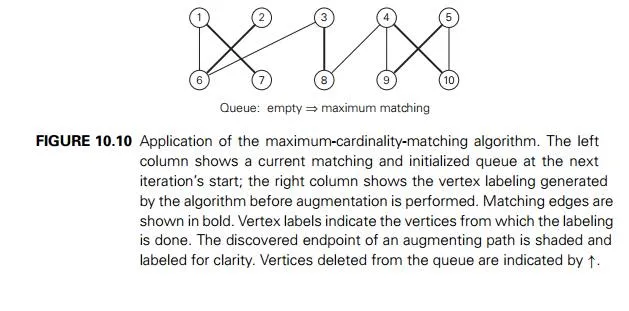
We now give a specific algorithm implementing this general template. We will search for an augmenting path for a matching M by a BFS-like traversal of the graph that starts simultaneously at all the free vertices in one of the sets V and U, say, V . (It would be logical to select the smaller of the two vertex sets, but we will ignore this observation in the pseudocode below.) Recall that an augmenting path, if it exists, is an odd-length path that connects a free vertex in V with a free vertex in U and which, unless it consists of a single edge, “zigs” from a vertex in V to another vertex’ mate in U , then “zags” back to V along the uniquely defined edge from M, and so on until a free vertex in U is reached. (Draw augmenting paths for the matchings in Figure 10.9, for example.) Hence, any candidate to be such a path must have its edges alternate in the pattern just described. This motivates the following rules for labeling vertices during the BFS-like traversal of the graph.
Case 1 (the queue’s front vertexw is inV ) Ifu is a free vertex adjacent tow, it is used as the other endpoint of an augmenting path; so the labeling stops and augmentation of the matching commences. The augmenting path in question is obtained by moving backward along the vertex labels (see below) to alternately add and delete its edges to and from the current matching. If u is not free and connected to w by an edge not in M, label u with w unless it has been already labeled.
Case 2 (the front vertexw is inU ) In this case,w must be matched and welabel its mate in V with w.
Here is pseudocode of the algorithm in its entirety.
ALGORITHM MaximumBipartiteMatching(G)
//Finds a maximum matching in a bipartite graph by a BFS-like traversal //Input: A bipartite graph G = V , U, E
//Output: A maximum-cardinality matching M in the input graph initialize set M of edges with some valid matching (e.g., the empty set) initialize queue Q with all the free vertices in V (in any order)
queue Q with all the free vertices in V (in any order)
while not Empty(Q) do
w ← Front(Q); Dequeue(Q)
if w ∈ V
for every vertex u adjacent to w do
if u is free
//augment
M ← M ∪ (w, u)
v ← w
while v is labeled do M ← M − (v, u)
u ← vertex indicated by v’s label;
v ← vertex indicated by u’s label; M ← M ∪ (v, u)
remove all vertex labels
reinitialize Q with all free vertices in V
break //exit the for loop
else //u is matched
if (w, u) ∈ M and u is unlabeled
label u with w
Enqueue(Q, u)
else //w ∈ U (and matched)
label the mate v of w with w
Enqueue(Q, v)
return M //current matching is maximum
An application of this algorithm to the matching in Figure 10.9a is shown in Figure 10.10. Note that the algorithm finds a maximum matching that differs from the one in Figure 10.9d.
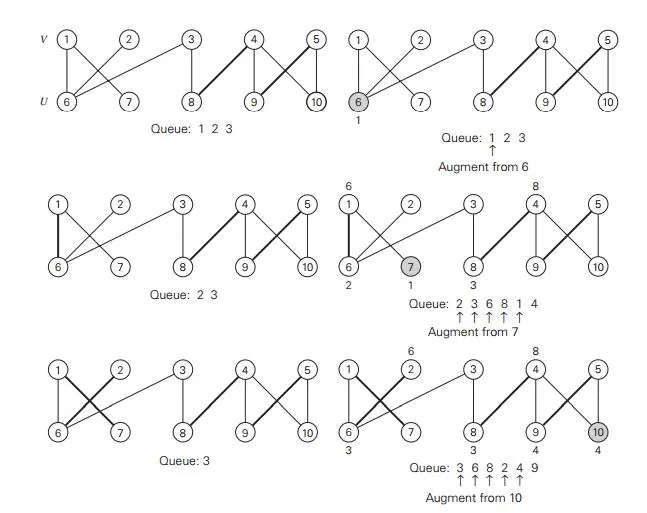
How efficient is the maximum-matching algorithm? Each iteration except the last one matches two previously free vertices—one from each of the sets V and U. Therefore, the total number of iterations cannot exceed n/2 + 1, where n = |V | + |U |is the number of vertices in the graph. The time spent on each iteration is in O(n + m), where m = |E| is the number of edges in the graph. (This assumes that the information about the status of each vertex—free or matched and the vertex’ mate if the latter—can be retrieved in constant time, e.g., by storing it in
an array.) Hence, the time efficiency of the algorithm is in O(n(n + m)). Hopcroft
 and Karp [Hop73] showed how the efficiency can be improved to O( n(n + m)) by combining several iterations into a single stage to maximize the number of edges added to the matching with one search.
and Karp [Hop73] showed how the efficiency can be improved to O( n(n + m)) by combining several iterations into a single stage to maximize the number of edges added to the matching with one search.
We were concerned in this section with matching the largest possible number of vertex pairs in a bipartite graph. Some applications may require taking into ac-count the quality or cost of matching different pairs. For example, workers may execute jobs with different efficiencies, or girls may have different preferences for their potential dance partners. It is natural to model such situations by bipartite graphs with weights assigned to their edges. This leads to the problem of maxi-mizing the sum of the weights on edges connecting matched pairs of vertices. This problem is called maximum-weight matching. We encountered it under a differ-ent name—the assignment problem—in Section 3.4. There are several sophisti-cated algorithms for this problem, which are much more efficient than exhaustive search (see, e.g., [Pap82], [Gal86], [Ahu93]). We have to leave them outside of our discussion, however, because of their complexity, especially for general graphs.
Exercises 10.3
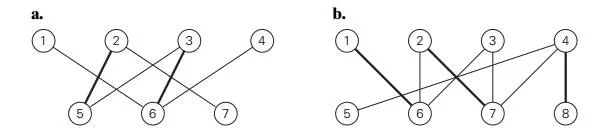
For each matching shown below in bold, find an augmentation or explain why no augmentation exists.
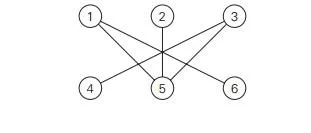
2. Apply the maximum-matching algorithm to the following bipartite graph:
a. What is the largest and what is the smallest possible cardinality of a matching in a bipartite graph G = V , U, E with n vertices in each vertex set V and U and at least n edges?
What is the largest and what is the smallest number of distinct solutions the maximum-cardinality-matching problem can have for a bipartite graph G = V , U, E with n vertices in each vertex set V and U and at least n edges?
a. Hall’s Marriage Theorem asserts that a bipartite graphG = V , U, E has amatching that matches all vertices of the set V if and only if for each subset S ⊆ V , |R(S)| ≥ |S|where R(S) is the set of all vertices adjacent to a vertex in S. Check this property for the following graph with (i) V = {1, 2, 3, 4} and (ii) V = {5, 6, 7}.
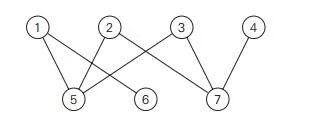
You have to devise an algorithm that returns yes if there is a matching in a bipartite graph G = V , U, E that matches all vertices in V and returns no otherwise. Would you base your algorithm on checking the condition of Hall’s Marriage Theorem?
Suppose there are five committees A, B, C, D, and E composed of six persons a, b, c, d, e, and f as follows: committee A’s members are b and e; committee B’s members are b, d, and e; committee C’s members are a, c, d, e, and f ; committee D’s members are b, d, and e; committee E’s members are b and e. Is there a system of distinct representatives, i.e., is it possible to select a representative from each committee so that all the selected persons are distinct?
Show how the maximum-cardinality-matching problem for a bipartite graph can be reduced to the maximum-flow problem discussed in Section 10.2.
Consider the following greedy algorithm for finding a maximum matching in a bipartite graph G = V , U, E . Sort all the vertices in nondecreasing order of their degrees. Scan this sorted list to add to the current matching (initially empty) the edge from the list’s free vertex to an adjacent free vertex of the lowest degree. If the list’s vertex is matched or if there are no adjacent free vertices for it, the vertex is simply skipped. Does this algorithm always produce a maximum matching in a bipartite graph?
Design a linear-time algorithm for finding a maximum matching in a tree.
Implement the maximum-matching algorithm of this section in the language of your choice. Experiment with its performance on bipartite graphs with n vertices in each of the vertex sets and randomly generated edges (in both dense and sparse modes) to compare the observed running time with the algorithm’s theoretical efficiency.
Domino puzzle A domino is a 2× 1 tile that can be oriented either hori-zontally or vertically. A tiling of a given board composed of 1 × 1 squares is covering it with dominoes exactly and without overlap. Is it possible to tile with dominoes an 8 × 8 board without two unit squares at its diagonally opposite corners?


Comments are closed