Finite automata may have outputs corresponding to each transition. There are two types of finite state machines that generate output −
- Mealy Machine
- Moore machine
Mealy Machine
A Mealy Machine is an FSM whose output depends on the present state as well as the present input.
It can be described by a 6 tuple (Q, ∑, O, δ, X, q0) where −
· Q is a finite set of states.
· ∑ is a finite set of symbols called the input alphabet.
· O is a finite set of symbols called the output alphabet.
· δ is the input transition function where δ: Q × ∑ → Q
· X is the output transition function where X: Q × ∑ → O
· q0 is the initial state from where any input is processed (q0 ∈ Q).
The state table of a Mealy Machine is shown below −
| Present state | Next state | |||
| input = 0 | input = 1 | |||
| State | Output | State | Output | |
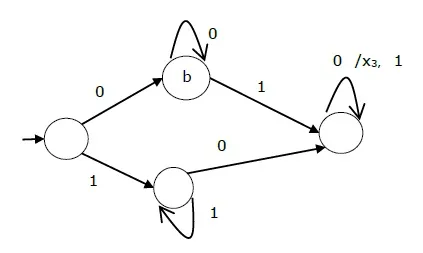
| → a | b | x1 | c | x1 |
| b | b | x2 | d | x3 |
| c | d | x3 | c | x1 |
| d | d | x3 | d | x2 |
The state diagram of the above Mealy Machine is −
Moore Machine
Moore machine is an FSM whose outputs depend on only the present state.
A Moore machine can be described by a 6 tuple (Q, ∑, O, δ, X, q0) where −
· Q is a finite set of states.
· ∑ is a finite set of symbols called the input alphabet.
· O is a finite set of symbols called the output alphabet.
· δ is the input transition function where δ: Q × ∑ → Q
· X is the output transition function where X: Q → O
· q0 is the initial state from where any input is processed (q0 ∈ Q).
The state table of a Moore Machine is shown below −
| Present state | Next State | Output | |
| Input = 0 | Input = 1 | ||
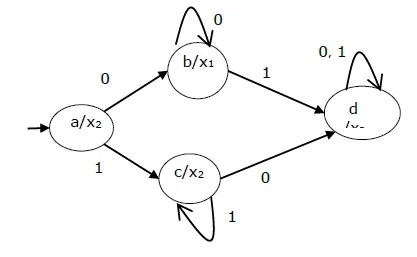
| → a | b | c | x2 |
| b | b | d | x1 |
| c | c | d | x2 |
| d | d | d | x3 |
The state diagram of the above Moore Machine is −
Mealy Machine vs. Moore Machine
The following table highlights the points that differentiate a Mealy Machine from a Moore Machine.
| Mealy Machine | Moore Machine |
| Output depends both upon the present state and the present input | Output depends only upon the present state. |
| Generally, it has fewer states than Moore Machine. | Generally, it has more states than Mealy Machine. |
| The value of the output function is a function of the transitions and the changes, when the input logic on the present state is done. | The value of the output function is a function of the current state and the changes at the clock edges, whenever state changes occur. |
| Mealy machines react faster to inputs. They generally react in the same clock cycle. | In Moore machines, more logic is required to decode the outputs resulting in more circuit delays. They generally react one clock cycle later. |
Moore Machine to Mealy Machine
Algorithm 4
Input − Moore Machine
Output − Mealy Machine
Step 1 − Take a blank Mealy Machine transition table format.
Step 2 − Copy all the Moore Machine transition states into this table format.
Step 3 − Check the present states and their corresponding outputs in the Moore Machine state table; if for a state Qi output is m, copy it into the output columns of the Mealy Machine state table wherever Qi appears in the next state.
Example
Let us consider the following Moore machine −
| Present State | Next State | Output | |
| a = 0 | a = 1 | ||
| → a | d | b | 1 |
| b | a | d | 0 |
| c | c | c | 0 |
| d | b | a | 1 |
Now we apply Algorithm 4 to convert it to Mealy Machine.
Step 1 & 2 −
| Present State | Next State | |||
| a = 0 | a = 1 | |||
| State | Output | State | Output | |
| → a | d | b | ||
| b | a | d | ||
| c | c | c | ||
| d | b | a |
Step 3 −
| Present State | Next State | |||
| a = 0 | a = 1 | |||
| State | Output | State | Output | |
| => a | d | 1 | b | 0 |
| b | a | 1 | d | 1 |
| c | c | 0 | c | 0 |
| d | b | 0 | a | 1 |
Mealy Machine to Moore Machine
Algorithm 5
Input − Mealy Machine
Output − Moore Machine
Step 1 − Calculate the number of different outputs for each state (Qi) that are available in the state table of the Mealy machine.
Step 2 − If all the outputs of Qi are same, copy state Qi. If it has n distinct outputs, break Qi into n states as Qin where n = 0, 1, 2…….
Step 3 − If the output of the initial state is 1, insert a new initial state at the beginning which gives 0 output.
Example
Let us consider the following Mealy Machine −
| Present State | Next State | |||
| a = 0 | a = 1 | |||
| Next State | Output | Next State | Output | |
| → a | d | 0 | b | 1 |
| b | a | 1 | d | 0 |
| c | c | 1 | c | 0 |
| d | b | 0 | a | 1 |
Here, states ‘a’ and ‘d’ give only 1 and 0 outputs respectively, so we retain states ‘a’ and ‘d’. But states ‘b’ and ‘c’ produce different outputs (1 and 0). So, we divide b into b0, b1 and c into c0, c1.
| Present State | Next State | Output | |
| a = 0 | a = 1 | ||
| → a | d | b1 | 1 |
| b0 | a | d | 0 |
| b1 | a | d | 1 |
| c0 | c1 | C0 | 0 |
| c1 | c1 | C0 | 1 |
| d | b0 | a | 0 |

