Among the types of modulation techniques, the main classification is Continuous-wave Modulation and Pulse Modulation. The continuous wave modulation techniques are further divided into Amplitude Modulation and Angle Modulation.
A continuous-wave goes on continuously without any intervals and it is the baseband message signal, which contains the information. This wave has to be modulated.
According to the standard definition, “The amplitude of the carrier signal varies in accordance with the instantaneous amplitude of the modulating signal.” Which means, the amplitude of the carrier signal which contains no information varies as per the amplitude of the signal, at each instant, which contains information. This can be well explained by the following figures.
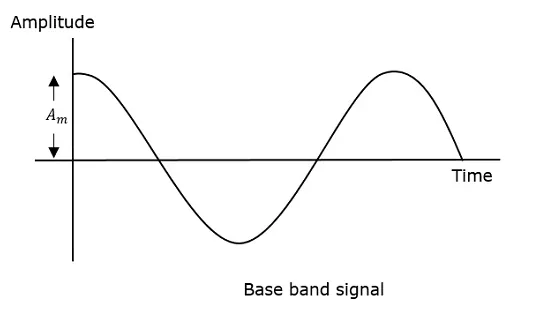
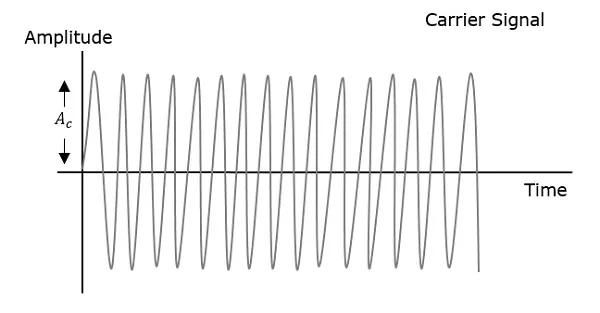
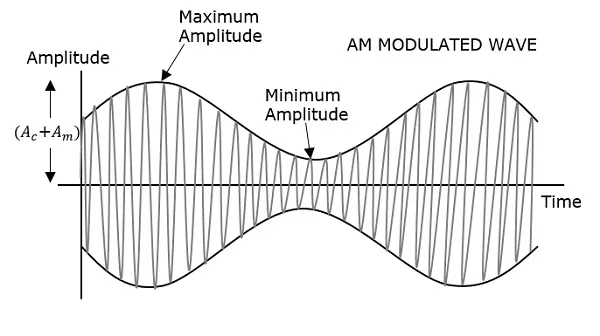
The modulating wave which is shown first is the message signal. The next one is the carrier wave, which is just a high frequency signal and contains no information. While the last one is the resultant modulated wave.
It can be observed that the positive and negative peaks of the carrier wave, are interconnected with an imaginary line. This line helps recreating the exact shape of the modulating signal. This imaginary line on the carrier wave is called as Envelope. It is the same as the message signal.
Mathematical Expression
Following are the mathematical expression for these waves.
Time-domain Representation of the Waves
Let modulating signal be −
$$m(t) = A_mcos(2\pi f_mt)$$
Let carrier signal be −
$$c(t) = A_ccos(2\pi f_ct)$$
Where Am = maximum amplitude of the modulating signal
Ac = maximum amplitude of the carrier signal
The standard form of an Amplitude Modulated wave is defined as −
$$S(t) = A_c[1+K_am(t)]cos(2\pi f_ct)$$
$$S(t) = A_c[1+\mu cos(2\pi f_mt)]cos(2\pi f_ct)$$
$$Where,\mu = K_aA_m$$
Modulation Index
A carrier wave, after being modulated, if the modulated level is calculated, then such an attempt is called as Modulation Index or Modulation Depth. It states the level of modulation that a carrier wave undergoes.
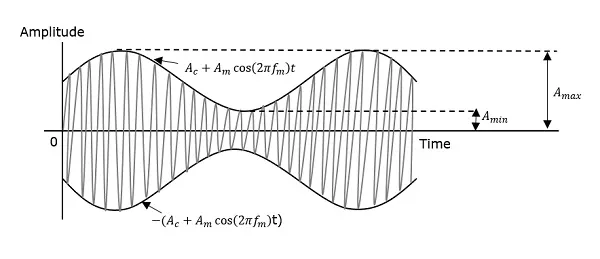
The maximum and minimum values of the envelope of the modulated wave are represented by Amax and Amin respectively.
Let us try to develop an equation for the Modulation Index.
$$A_{max} = A_c(1+\mu )$$
Since, at Amax the value of cos θ is 1
$$A_{min} = A_c(1-\mu )$$
Since, at Amin the value of cos θ is -1
$$\frac{A_{max}}{A_{min}} = \frac{1+\mu }{1-\mu }$$
$$A_{max}-\mu A_{max} = A_{min}+\mu A_{min}$$
$$-\mu (A_{max}+A_{min}) = A_{min}-A_{max}$$
$$\mu = \frac{A_{max}-A_{min}}{A_{max}+A_{min}}$$
Hence, the equation for Modulation Index is obtained. µ denotes the modulation index or modulation depth. This is often denoted in percentage called as Percentage Modulation. It is the extent of modulation denoted in percentage, and is denoted by m.
For a perfect modulation, the value of modulation index should be 1, which means the modulation depth should be 100%.
For instance, if this value is less than 1, i.e., the modulation index is 0.5, then the modulated output would look like the following figure. It is called as Under-modulation. Such a wave is called as an under-modulated wave.
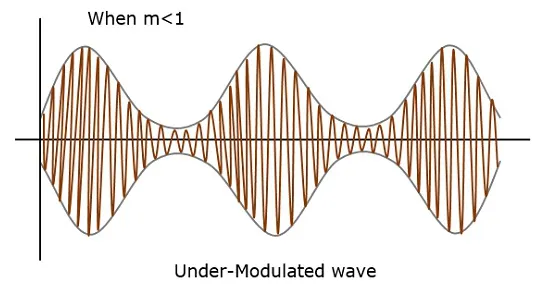
If the value of the modulation index is greater than 1, i.e., 1.5 or so, then the wave will be an over-modulated wave. It would look like the following figure.
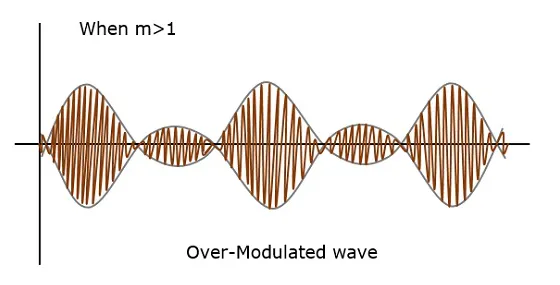
As the value of modulation index increases, the carrier experiences a 180° phase reversal, which causes additional sidebands and hence, the wave gets distorted. Such overmodulated wave causes interference, which cannot be eliminated.
Bandwidth of Amplitude Modulation
The bandwidth is the difference between lowest and highest frequencies of the signal.
For amplitude modulated wave, the bandwidth is given by
$$BW = f_{USB}-f_{LSB}$$
$$(f_c+f_m)-(f_c-f_m)$$
$$ = 2f_m = 2W$$
Where W is the message bandwidth
Hence we got to know that the bandwidth required for the amplitude modulated wave is twice the frequency of the modulating signal.

