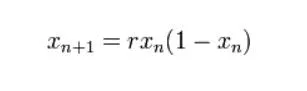Fundamentals of Analysis of Algorithm:
1 Analysis of Framework
2 Measuring an input size
3 Units for measuring runtime
4 Worst case, Best case and Average case
5 Asymptotic Notations
1 ANALYSIS FRAME WORK
♦ there are two kinds of efficiency
♦ Time efficiency – indicates how fast an algorithm in question runs.
♦ Space efficiency – deals with the extra space the algorithm requires.
2 MEASURING AN INPUT SIZE
♦ An algorithm’s efficiency as a function of some parameter n indicating the algorithm’s input size.
♦ In most cases, selecting such a parameter is quite straightforward.
♦ For example, it will be the size of the list for problems of sorting, searching, finding the list’s smallest element, and most other problems dealing with lists.
♦ For the problem of evaluating a polynomial p(x) = a n x n+ . . . + a 0 of degree n, it will be the polynomial’s degree or the number of its coefficients, which is larger by one than its degree.
♦ There are situations, of course, where the choice of a parameter indicating an input size does matter.
♦ Example – computing the product of two n-by-n matrices.
♦ There are two natural measures of size for this problem.
♦ The matrix order n.
♦ The total number of elements N in the matrices being multiplied.
♦ Since there is a simple formula relating these two measures, we can easily switch from one to the other, but the answer about an algorithm’s efficiency will be qualitatively different depending on which of the two measures we use.
♦ The choice of an appropriate size metric can be influenced by operations of the algorithm in question. For example, how should we measure an input’s size for a spell-checking algorithm? If the algorithm examines individual characters of its input, then we should measure the size by the number of characters; if it works by processing words, we should count their number in the input.
♦ We should make a special note about measuring size of inputs for algorithms involving properties of numbers (e.g., checking whether a given integer n is prime).
♦ For such algorithms, computer scientists prefer measuring size by the number b of bits in the n’s binary representation:
b=|log2n|+1

♦ This metric usually gives a better idea about efficiency of algorithms in question.
3 UNITS FOR MEASURING RUN TIME:
♦ We can simply use some standard unit of time measurement-a second, a millisecond, and so on-to measure the running time of a program implementing the algorithm.
♦ There are obvious drawbacks to such an approach. They are
♦ Dependence on the speed of a particular computer
♦ Dependence on the quality of a program implementing the algorithm
♦ The compiler used in generating the machine code
♦ The difficulty of clocking the actual running time of the program.
♦ Since we are in need to measure algorithm efficiency, we should have a metric that does not depend on these extraneous factors.
♦ One possible approach is to count the number of times each of the algorithm’s operations is executed. This approach is both difficult and unnecessary.
♦ The main objective is to identify the most important operation of the algorithm, called the basic operation, the operation contributing the most to the total running time, and compute the number of times the basic operation is executed.
4 WORST CASE, BEST CASE AND AVERAGE CASE EFFICIENCES
♦ It is reasonable to measure an algorithm’s efficiency as a function of a parameter indicating the size of the algorithm’s input.
♦ But there are many algorithms for which running time depends not only on an input size but also on the specifics of a particular input.
♦ Example, sequential search. This is a straightforward algorithm that searches for agiven item (some search key K) in a list of n elements by checking successive elements of the list until either a match with the search key is found or the list is exhausted.
♦ Here is the algorithm’s pseudo code, in which, for simplicity, a list is implemented as an array. (It also assumes that the second condition A[i] i= K will not be checked if the first one, which checks that the array’s index does not exceed its upper bound, fails.)
ALGORITHM Sequential Search(A[0..n -1], K)
//Searches for a given value in a given array by sequential search //Input: An array A[0..n -1] and a search key K
//Output: Returns the index of the first element of A that matches K // or -1 ifthere are no matching elements
i←0
while i < n and A[i]≠K do
i←i+1
if i < n return i else return -1
♦ Clearly, the running time of this algorithm can be quite different for the same list size n.
Worst case efficiency
♦ The worst-case efficiency of an algorithm is its efficiency for the worst-case input of size n, which is an input (or inputs) of size n for which the algorithm runs the longest among all possible inputs of that size.
♦ In the worst case, when there are no matching elements or the first matching element happens to be the last one on the list, the algorithm makes the largest number of key comparisons among all possible inputs of size n:
Cworst (n) = n.
♦ The way to determine is quite straightforward
♦ To analyze the algorithm to see what kind of inputs yield the largest value of the basic operation’s count C(n) among all possible inputs of size n and then compute this worst-case value C worst (n)
♦ The worst-case analysis provides very important information about an algorithm’s efficiency by bounding its running time from above. In other words, it guarantees that for any instance of size n, the running time will not exceed C worst (n) its running time on the worst-case inputs.
Best case Efficiency
♦ The best-case efficiency of an algorithm is its efficiency for the best-case input of size n, which is an input (or inputs) of size n for which the algorithm runs the fastest among all possible inputs of that size.
♦ We can analyze the best case efficiency as follows.
♦ First, determine the kind of inputs for which the count C (n) will be the smallest among all possible inputs of size n. (Note that the best case does not mean the smallest input; it means the input of size n for which the algorithm runs the fastest.)
♦ Then ascertain the value of C (n) on these most convenient inputs.
♦ Example- for sequential search, best-case inputs will be lists of size n with their first elements equal to a search key; accordingly, Cbest(n) = 1.
♦ The analysis of the best-case efficiency is not nearly as important as that of the worst-case efficiency.
♦ But it is not completely useless. For example, there is a sorting algorithm (insertion sort) for which the best-case inputs are already sorted arrays on which the algorithm works very fast.
♦ Thus, such an algorithm might well be the method of choice for applications dealing with almost sorted arrays. And, of course, if the best-case efficiency of an algorithm is unsatisfactory, we can immediately discard it without further analysis.
Average case efficiency
♦ It yields the information about an algorithm about an algorithm‘s behaviour on a ―typical‖ and ―random‖ input.
♦ To analyze the algorithm’s average-case efficiency, we must make some assumptions about possible inputs of size n.
♦ The investigation of the average case efficiency is considerably more difficult than investigation of the worst case and best case efficiency.
♦ It involves dividing all instances of size n .into several classes so that for each instance of the class the number of times the algorithm’s basic operation is executed is the same.
♦ Then a probability distribution of inputs needs to be obtained or assumed so that the expected value of the basic operation’s count can then be derived.
The average number of key comparisions Cavg(n) can be computed as follows,
♦ let us consider again sequential search. The standard assumptions are,
♦ In the case of a successful search, the probability of the first match occurring in the ith position of the list is pin for every i, and the number of comparisons made by the algorithm in such a situation is obviously i.
♦ In the case of an unsuccessful search, the number of comparisons is n with the probability of such a search being (1 – p). Therefore,
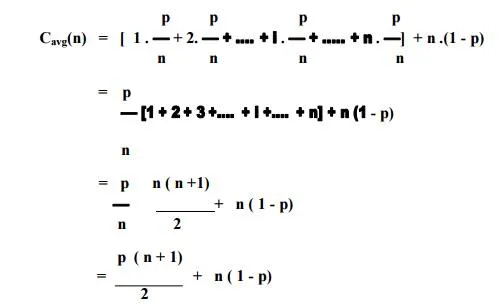
♦ Example, if p = 1 (i.e., the search must be successful), the average number of key comparisons made by sequential search is (n + 1) /2.
♦ If p = 0 (i.e., the search must be unsuccessful), the average number of key comparisons will be n because the algorithm will inspect all n elements on all such inputs.
5 Asymptotic Notations
Step count is to compare time complexity of two programs that compute same function and also to predict the growth in run time as instance characteristics changes. Determining exact step count is difficult and not necessary also. Because the values are not exact quantities. We need only comparative statements like c1n2 ≤ tp(n) ≤ c2n2.
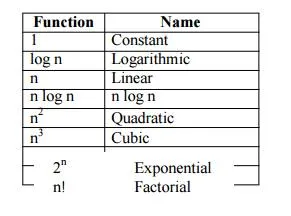
For example, consider two programs with complexities c1n2 + c2n and c3n respectively. For small values of n, complexity depend upon values of c1, c2 and c3. But there will also be an n beyond which complexity of c3n is better than that of c1n2 + c2n.This value of n is called break-even point. If this point is zero, c 3n is always faster (or at least as fast). Common asymptotic functions are given below.
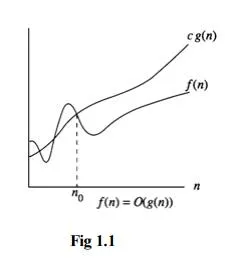
Big‘Oh’Notation(O)
O(g(n)) = { f(n) : there exist positive constants c and n0 such that 0 ≤ f(n) ≤ cg(n) for all n ≥
n0 }
It is the upper bound of any function. Hence it denotes the worse case complexity of any algorithm. We can represent it graphically as
Find the Big ‗Oh‘ for the following functions:
Linear Functions
Example 1.6 f(n) = 3n + 2
General form is f(n) ≤ cg(n)
When n ≥ 2, 3n + 2 ≤ 3n + n = 4n
Hence f(n) = O(n), here c = 4 and n0 = 2
When n ≥ 1, 3n + 2 ≤ 3n + 2n = 5n
Hence f(n) = O(n), here c = 5 and n0 = 1
Hence we can have different c,n0 pairs satisfying for a given function.
Example f(n) = 3n + 3
When n ≥ 3, 3n + 3 ≤ 3n + n = 4n Hence f(n) = O(n), here c = 4 and n0 = 3
Example
f(n) = 100n + 6
When n ≥ 6, 100n + 6 ≤ 100n + n = 101n Hence f(n) = O(n), here c = 101 and n0 = 6
Quadratic Functions
Example 1.9
f(n) = 10n2 + 4n + 2
When n ≥ 2, 10n2 + 4n + 2 ≤ 10n2 + 5n
When n ≥ 5, 5n ≤ n2, 10n2 + 4n + 2 ≤ 10n2 + n2 = 11n2 Hence f(n) = O(n2), here c = 11 and n0 = 5
Example 1.10
f(n) = 1000n2 + 100n – 6
f(n) ≤ 1000n2 + 100n for all values of n.
When n ≥ 100, 5n ≤ n2, f(n) ≤ 1000n2 + n2 = 1001n2 Hence f(n) = O(n2), here c = 1001 and n0 = 100
Exponential Functions
Example 1.11 f(n) = 6*2n + n2
When n ≥ 4, n2 ≤ 2n
So f(n) ≤ 6*2n + 2n = 7*2n
Hence f(n) = O(2n), here c = 7 and n0 = 4
Constant Functions
Example 1.12 f(n) = 10
f(n) = O(1), because f(n) ≤ 10*1
OmegaNotation(Ω)
Ω (g(n)) = { f(n) : there exist positive constants c and n0 such that 0 ≤ cg(n) ≤ f(n) for all n
≥ n0 }
It is the lower bound of any function. Hence it denotes the best case complexity of any algorithm. We can represent it graphically as
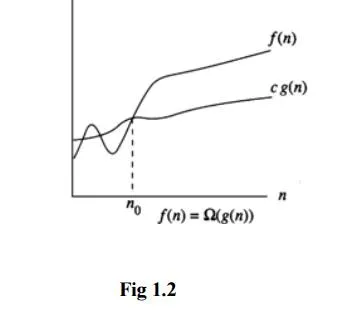
Example 1.13 f(n) = 3n + 2
3n + 2 > 3n for all n. Hence f(n) = Ω(n)
Similarly we can solve all the examples specified under Big ‗Oh‘.
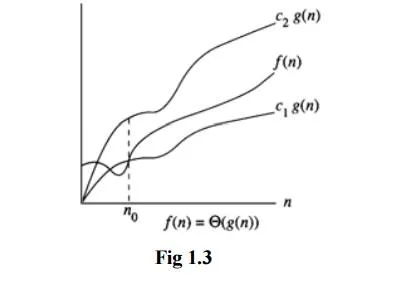
ThetaNotation(Θ)

Θ(g(n)) = {f(n) : there exist positive constants c1,c2 and n0 such that c1g(n) ≤f(n) ≤c2g(n) for all n ≥ n0 }
If f(n) = Θ(g(n)), all values of n right to n0 f(n) lies on or above c1g(n) and on or below c2g(n). Hence it is asymptotic tight bound for f(n).
Little-O Notation
For non-negative functions, f(n) and g(n), f(n) is little o of g(n) if and only if f(n) = O(g(n)), but f(n) ≠ Θ(g(n)). This is denoted as “f(n) = o(g(n))”.
This represents a loose bounding version of Big O. g(n) bounds from the top, but it does not bound the bottom.
Little Omega Notation
For non-negative functions, f(n) and g(n), f(n) is little omega of g(n) if and only if f(n) = Ω(g(n)), but f(n) ≠ Θ(g(n)). This is denoted as “f(n) = ω(g(n))”.
Much like Little Oh, this is the equivalent for Big Omega. g(n) is a loose lower boundary of the function f(n); it bounds from the bottom, but not from the top.
Conditional asymptotic notation
Many algorithms are easier to analyse if initially we restrict our attention to instances whose size satisfies a certain condition, such as being a power of 2. Consider, for example, the divide and conquer algorithm for multiplying large integers that we saw in the Introduction. Let n be the size of the integers to be multiplied.
The algorithm proceeds directly if n = 1, which requires a microseconds for an appropriate constant a. If n>1, the algorithm proceeds by multiplying four pairs of integers of size  three if we use the better algorithm). Moreover, it takes a linear amount of time to carry out additional tasks. For simplicity, let us say that the additional work takes at most bn microseconds for an appropriate constant b.
three if we use the better algorithm). Moreover, it takes a linear amount of time to carry out additional tasks. For simplicity, let us say that the additional work takes at most bn microseconds for an appropriate constant b.

Properties of Big-Oh Notation
Generally, we use asymptotic notation as a convenient way to examine what can happen in a function in the worst case or in the best case. For example, if you want to write a function that searches through an array of numbers and returns the smallest one:
function find-min(array a[1..n]) let j :=
for i := 1 to n:
j := min(j, a[i] ) repeat
return j end
Regardless of how big or small the array is, every time we run find-min, we have to initialize the i and j integer variables and return j at the end. Therefore, we can just think of those parts of the function as constant and ignore them.
So, how can we use asymptotic notation to discuss the find-min function? If we search through an array with 87 elements, then the for loop iterates 87 times, even if the very first element we hit turns out to be the minimum. Likewise, for n elements, the for loop iterates n times. Therefore we say the function runs in time O(n).
function find-min-plus-max(array a[1..n] )
// First, find the smallest element in the array let j := ;
for i := 1 to n:
j := min(j, a[i] ) repeat
let minim := j
// Now, find the biggest element, add it to the smallest and j := ;
for i := 1 to n:
j := max(j, a[i] ) repeat
let maxim := j
// return the sum of the two return minim + maxim;
end
What’s the running time for find-min-plus-max? There are two for loops, that each iterate n times, so the running time is clearly O(2n). Because 2 is a constant, we throw it away and write the running time as O(n). Why can you do this? If you recall the definition of Big-O notation, the function whose bound you’re testing can be multiplied by some constant. If f(x)=2x, we can see that if g(x) = x, then the Big-O condition holds. Thus O(2n) = O(n). This rule is general for the various asymptotic notations.
Recurrence
When an algorithm contains a recursive call to itself, its running time can often be described by a recurrence
Recurrence Equation
A recurrence relation is an equation that recursively defines a sequence. Each term of the sequence is defined as a function of the preceding terms. A difference equation is a specific type of recurrence relation.
An example of a recurrence relation is the logistic map: