Independent sets are represented in sets, in which
· there should not be any edges adjacent to each other. There should not be any common vertex between any two edges.
· there should not be any vertices adjacent to each other. There should not be any common edge between any two vertices.
Independent Line Set
Let ‘G’ = (V, E) be a graph. A subset L of E is called an independent line set of ‘G’ if no two edges in L are adjacent. Such a set is called an independent line set.
Example
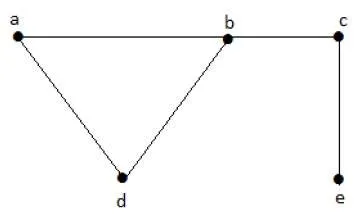
Let us consider the following subsets −
L1 = {a,b}
L2 = {a,b} {c,e}
L3 = {a,d} {b,c}
In this example, the subsets L2 and L3 are clearly not the adjacent edges in the given graph. They are independent line sets. However L1 is not an independent line set, as for making an independent line set, there should be at least two edges.
Maximal Independent Line Set
An independent line set is said to be the maximal independent line set of a graph ‘G’ if no other edge of ‘G’ can be added to ‘L’.
Example
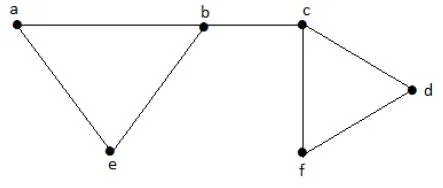
Let us consider the following subsets −
L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}
L2 and L3 are maximal independent line sets/maximal matching. As for only these two subsets, there is no chance of adding any other edge which is not an adjacent. Hence these two subsets are considered as the maximal independent line sets.
Maximum Independent Line Set
A maximum independent line set of ‘G’ with maximum number of edges is called a maximum independent line set of ‘G’.
Number of edges in a maximum independent line set of G (β1)
= Line independent number of G
= Matching number of G
Example
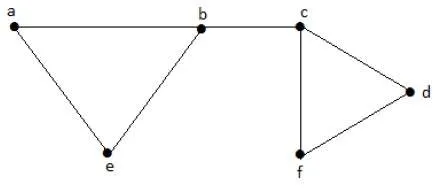
Let us consider the following subsets −
L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}
L3 is the maximum independent line set of G with maximum edges which are not the adjacent edges in graph and is denoted by β1 = 3.
Note − For any graph G with no isolated vertex,
α1 + β1 = number of vertices in a graph = |V|
Example
Line covering number of Kn/Cn/wn,
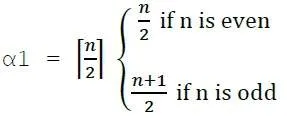
Line independent number (Matching number) = β1 = ⌊n2⌋ α1 + β1 = n
Independent Vertex Set
Let ‘G’ = (V, E) be a graph. A subset of ‘V’ is called an independent set of ‘G’ if no two vertices in ‘S’ are adjacent.
Example
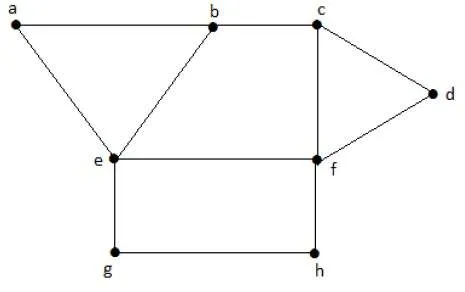
Consider the following subsets from the above graphs −
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}
Clearly S1 is not an independent vertex set, because for getting an independent vertex set, there should be at least two vertices in the from a graph. But here it is not that case. The subsets S2, S3, and S4 are the independent vertex sets because there is no vertex that is adjacent to any one vertex from the subsets.
Maximal Independent Vertex Set
Let ‘G’ be a graph, then an independent vertex set of ‘G’ is said to be maximal if no other vertex of ‘G’ can be added to ‘S’.
Example
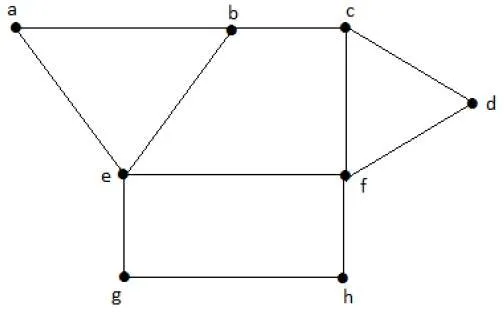
Consider the following subsets from the above graphs.
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}
S2 and S3 are maximal independent vertex sets of ‘G’. In S1 and S4, we can add other vertices; but in S2 and S3, we cannot add any other vertex
Maximum Independent Vertex Set
A maximal independent vertex set of ‘G’ with maximum number of vertices is called as the maximum independent vertex set.
Example
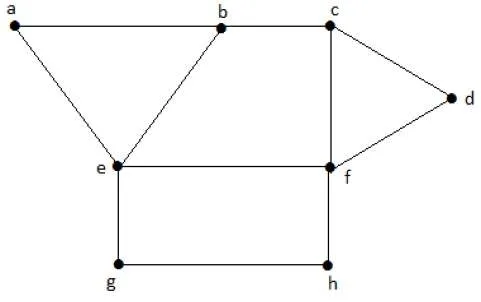
Consider the following subsets from the above graph −
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}
Only S3 is the maximum independent vertex set, as it covers the highest number of vertices. The number of vertices in a maximum independent vertex set of ‘G’ is called the independent vertex number of G (β2).
Example
For the complete graph Kn,
Vertex covering number = α2 = n−1
Vertex independent number = β2 = 1
You have α2 + β2 = n
In a complete graph, each vertex is adjacent to its remaining (n − 1) vertices. Therefore, a maximum independent set of Kn contains only one vertex.
Therefore, β2=1
and α2=|v| − β2 = n-1
Note − For any graph ‘G’ = (V, E)
· α2 + β2 = |v|
· If ‘S’ is an independent vertex set of ‘G’, then (V – S) is a vertex cover of G.
