In this chapter, we will cover a few standard examples to demonstrate the concepts we already discussed in the earlier chapters.
Example 1
Find the number of spanning trees in the following graph.
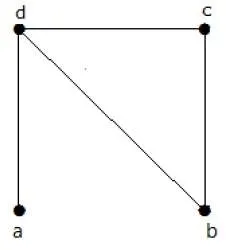
Solution
The number of spanning trees obtained from the above graph is 3. They are as follows −
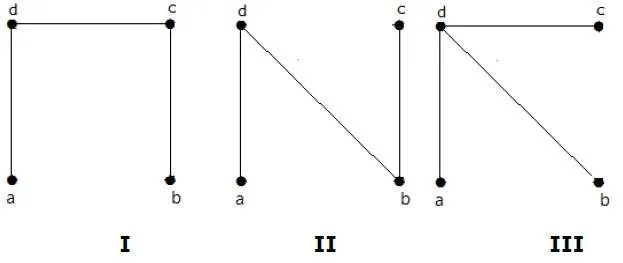
These three are the spanning trees for the given graphs. Here the graphs I and II are isomorphic to each other. Clearly, the number of non-isomorphic spanning trees is two.
Example 2
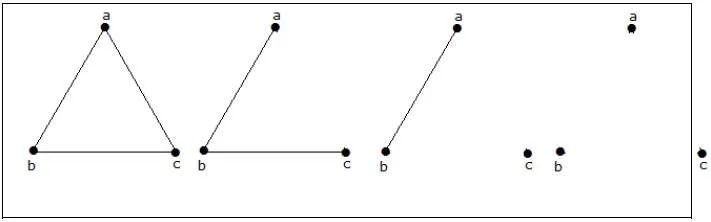
How many simple non-isomorphic graphs are possible with 3 vertices?
Solution
There are 4 non-isomorphic graphs possible with 3 vertices. They are shown below.
Example 3
Let ‘G’ be a connected planar graph with 20 vertices and the degree of each vertex is 3. Find the number of regions in the graph.
Solution
By the sum of degrees theorem,
20 ∑ i=1 deg(Vi) = 2|E|
20(3) = 2|E|
|E| = 30
By Euler’s formula,
|V| + |R| = |E| + 2
20+ |R| = 30 + 2
|R| = 12
Hence, the number of regions is 12.
Example 4
What is the chromatic number of complete graph Kn?
Solution
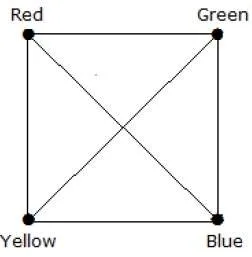
In a complete graph, each vertex is adjacent to is remaining (n–1) vertices. Hence, each vertex requires a new color. Hence the chromatic number Kn = n.
Example 5
What is the matching number for the following graph?
Solution
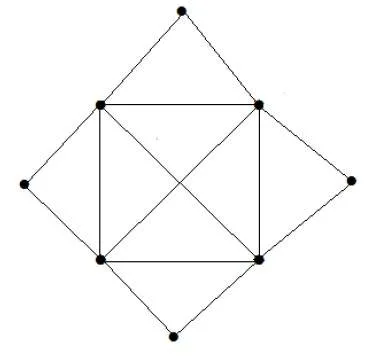
Number of vertices = 9
We can match only 8 vertices.
Matching number is 4.
Example 6
What is the line covering number of for the following graph?
Solution
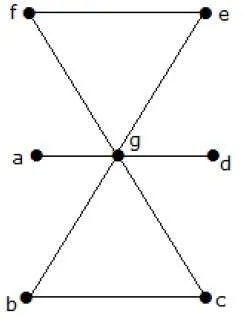
Number of vertices = |V| = n = 7
Line covering number = (α1) ≥ ⌈n2⌉ = 3
α1 ≥ 3
By using 3 edges, we can cover all the vertices.
Hence, the line covering number is 3.

