Not all graphs are planar. If there are too many edges and too few vertices, then some of the edges will need to intersect. The smallest graph where this happens is \(K_5\text{.}\)

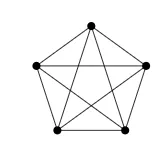
If you try to redraw this without edges crossing, you quickly get into trouble. There seems to be one edge too many. In fact, we can prove that no matter how you draw it, \(K_5\) will always have edges crossing.
Theorem 4.3.1.
\(K_5\) is not planar.
Proof.
The proof is by contradiction. So assume that \(K_5\) is planar. Then the graph must satisfy Euler’s formula for planar graphs. \(K_5\) has 5 vertices and 10 edges, so we get
\begin{equation*} 5 – 10 + f = 2\text{,} \end{equation*}
which says that if the graph is drawn without any edges crossing, there would be \(f = 7\) faces.
Now consider how many edges surround each face. Each face must be surrounded by at least 3 edges. Let \(B\) be the total number of boundaries around all the faces in the graph. Thus we have that \(3f \le B\text{.}\) But also \(B = 2e\text{,}\) since each edge is used as a boundary exactly twice. Putting this together we get
\begin{equation*} 3f \le 2e\text{.} \end{equation*}
But this is impossible, since we have already determined that \(f = 7\) and \(e = 10\text{,}\) and \(21 \not\le 20\text{.}\) This is a contradiction so in fact \(K_5\) is not planar.
The other simplest graph which is not planar is \(K_{3,3}\)

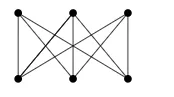
Proving that \(K_{3,3}\) is not planar answers the houses and utilities puzzle: it is not possible to connect each of three houses to each of three utilities without the lines crossing.
Theorem 4.3.2.
\(K_{3,3}\) is not planar.
Proof.
Again, we proceed by contradiction. Suppose \(K_{3,3}\) were planar. Then by Euler’s formula there will be 5 faces, since \(v = 6\text{,}\) \(e = 9\text{,}\) and \(6 – 9 + f = 2\text{.}\)
How many boundaries surround these 5 faces? Let \(B\) be this number. Since each edge is used as a boundary twice, we have \(B = 2e\text{.}\) Also, \(B \ge 4f\) since each face is surrounded by 4 or more boundaries. We know this is true because \(K_{3,3}\) is bipartite, so does not contain any 3-edge cycles. Thus
\begin{equation*} 4f \le 2e\text{.} \end{equation*}
But this would say that \(20 \le 18\text{,}\) which is clearly false. Thus \(K_{3,3}\) is not planar.
Note the similarities and differences in these proofs. Both are proofs by contradiction, and both start with using Euler’s formula to derive the (supposed) number of faces in the graph. Then we find a relationship between the number of faces and the number of edges based on how many edges surround each face. This is the only difference. In the proof for \(K_5\text{,}\) we got \(3f \le 2e\) and for \(K_{3,3}\) we go \(4f \le 2e\text{.}\) The coefficient of \(f\) is the key. It is the smallest number of edges which could surround any face. If some number of edges surround a face, then these edges form a cycle. So that number is the size of the smallest cycle in the graph.
In general, if we let \(g\) be the size of the smallest cycle in a graph (\(g\) stands for girth, which is the technical term for this) then for any planar graph we have \(gf \le 2e\text{.}\) When this disagrees with Euler’s formula, we know for sure that the graph cannot be planar.

