Source encoding theorem
The discrete memory less source of entropy H(X), the average code word length (L) for any distortion less source encoding is bounded.
Code redundancy is the measure of redundancy bits in the encoded message sequence.
Mutual information is the amount of information transferred when Xi is transmitted and Yi is received. It is represented by I(Xi,Yi) .The average mutual information is defined as the amount of source information gain per received symbol.
A block code of length n and 2k code words is calleda linear (n, k) code if and only if its 2k code words form a k-dimensional subspace of the vector space of all the n-tuples over the field GF(2). The message occurring frequently can be assigned short code words, whereas message which occur rarely are assigned long code word, such coding is called variable length coding.
The efficient representation of data generated by a discrete source is known as source encoding. This device that performs this representation is called source encoder.
The types of error control method
· Error detection and retransmission
· Error detection and correction
Channel capacity is defined as the maximum of the mutual information that may be transmitted through the channel.
The needs for encoding
To improve the efficiency of communication
To improve the transmission quality.
The entropy of a source is a measure of the average amount of information per source symbol in a long message. Channel coding theorem is applied for discrete memory less additive white gaussian noise channels.
The advantages of Shannon fano coding
1. Reduced bandwidth
2. Reduced noise
3. It can be used for error detection and correction.
The objectives of cyclic codes :
Encoding and syndrome calculations can be easily implemented by using simple shift register with feedback connection It is possible to design codes having useful error correction properties
Source Coding Theorem
The source coding theorem shows that (in the limit, as the length of a stream of independent and identically-distributed random variable (data tends to infinity) it is impossible to compress the data such that the code rate (average number of bits per symbol) is less than the Shannon entropy of the source, without it being virtually certain that information will be lost. However it is possible to get the code rate arbitrarily close to the Shannon entropy, with negligible probability of loss.
Proof: Source coding theorem
Given X is an i.i.d. source, its time series X1, …, Xn is i.i.d. with entropy H(X) in the discrete-valued case and differential entropy in the continuous-valued case. The Source coding theorem states that for any ε> 0 for any rate larger than the entropy of the source, there is large enough n and an encoder that takes n i.i.d. repetition of the source, X1:n, and maps it to n(H(X) +ε) binary bits such that the source symbols X1:nare recoverable from the binary bits withprobability at least 1- ε.
Proof of Achievability. Fix someε> 0, and let
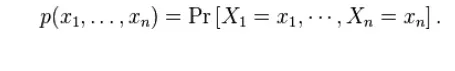
The typical set, Aεn,isdefined as follows:
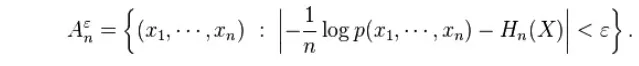
The Asymptotic Equipartition Property (AEP) shows that for large enough n, the probability that a sequence generated by the source lies in the typical set, Aεn,as defined approaches one. In particular there for large enough n,

The encoding algorithm: The encoder checks if the input sequence lies within the typical set; if yes, it outputs the index of the input sequence within the typical set; if not, the encoder outputs an arbitrary n(H(X) + ε)digit number. As long as the input sequence lies within the typical set (with probability at least 1- ε),the encoder doesn’t make any error. So, the probability of error of the encoder is bounded above by ε.
Proof of Converse. The converse is proved by showing that any set of size smaller than Aε
n (in the sense of exponent) would cover a set of probability bounded away from 1.
Proof: Source coding theorem for symbol codes

where the second line follows from Gibbs’ inequality and the fifth line follows from Kraft’s inequality:
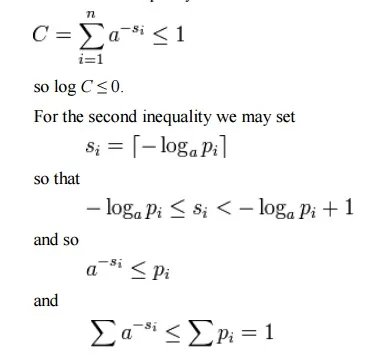
and so by Kraft’s inequality there exists a prefix-free code having those word lengths.
Thus the minimal S
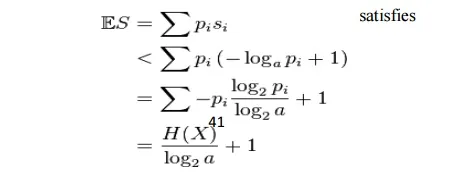


Comments are closed