In this section, we will see how to apply the general framework for analysis of algorithms to recursive algorithms. We start with an example often used to introduce novices to the idea of a recursive algorithm.
EXAMPLE 1 Compute the factorial function F (n) = n! for an arbitrary nonneg-ative integer n. Since
n! =1 . . . . . (n −1) . n = (n −1)! . n for n ≥ 1
and 0! = 1 by definition, we can compute F (n) = F (n − 1) . n with the following recursive algorithm.
ALGORITHM F(n)
//Computes n! recursively //Input: A nonnegative integer n //Output: The value of n!
if n = 0 return 1
else return F (n − 1) ∗ n
For simplicity, we consider n itself as an indicator of this algorithm’s input size (rather than the number of bits in its binary expansion). The basic operation of the algorithm is multiplication,5 whose number of executions we denote M(n). Since the function F (n) is computed according to the formula
F (n) = F (n −1) . n for n > 0,
the number of multiplications M(n) needed to compute it must satisfy the equality
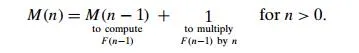
Indeed, M(n − 1) multiplications are spent to compute F (n − 1), and one more multiplication is needed to multiply the result by n.
The last equation defines the sequence M(n) that we need to find. This equa-tion defines M(n) not explicitly, i.e., as a function of n, but implicitly as a function of its value at another point, namely n − 1. Such equations are called recurrence relations or, for brevity, recurrences. Recurrence relations play an important rolenot only in analysis of algorithms but also in some areas of applied mathematics. They are usually studied in detail in courses on discrete mathematics or discrete structures; a very brief tutorial on them is provided in Appendix B. Our goal now is to solve the recurrence relation M(n) = M(n − 1) + 1, i.e., to find an explicit formula for M(n) in terms of n only.
Note, however, that there is not one but infinitely many sequences that satisfy this recurrence. (Can you give examples of, say, two of them?) To determine a solution uniquely, we need an initial condition that tells us the value with which the sequence starts. We can obtain this value by inspecting the condition that makes the algorithm stop its recursive calls:
if n = 0 return 1.
This tells us two things. First, since the calls stop when n = 0, the smallest value of n for which this algorithm is executed and hence M(n) defined is 0. Second, by inspecting the pseudocode’s exiting line, we can see that when n = 0, the algorithm performs no multiplications. Therefore, the initial condition we are after is

Before we embark on a discussion of how to solve this recurrence, let us pause to reiterate an important point. We are dealing here with two recursively defined functions. The first is the factorial function F (n) itself; it is defined by the recurrence
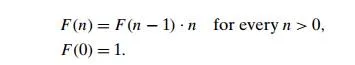
The second is the number of multiplications M(n) needed to compute F (n) by the recursive algorithm whose pseudocode was given at the beginning of the section.
As we just showed, M(n) is defined by recurrence (2.2). And it is recurrence (2.2) that we need to solve now.
Though it is not difficult to “guess” the solution here (what sequence starts with 0 when n = 0 and increases by 1 on each step?), it will be more useful to arrive at it in a systematic fashion. From the several techniques available for solving recurrence relations, we use what can be called the method of backward substitutions. The method’s idea (and the reason for the name) is immediatelyclear from the way it applies to solving our particular recurrence:
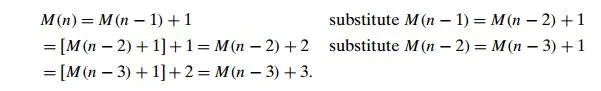
After inspecting the first three lines, we see an emerging pattern, which makes it possible to predict not only the next line (what would it be?) but also a general formula for the pattern: M(n) = M(n − i) + i. Strictly speaking, the correctness of this formula should be proved by mathematical induction, but it is easier to get to the solution as follows and then verify its correctness.
What remains to be done is to take advantage of the initial condition given. Since it is specified for n = 0, we have to substitute i = n in the pattern’s formula to get the ultimate result of our backward substitutions:
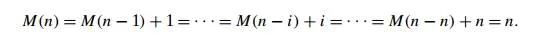
You should not be disappointed after exerting so much effort to get this “obvious” answer. The benefits of the method illustrated in this simple example will become clear very soon, when we have to solve more difficult recurrences. Also, note that the simple iterative algorithm that accumulates the product of n consecutive integers requires the same number of multiplications, and it does so without the overhead of time and space used for maintaining the recursion’s stack.
The issue of time efficiency is actually not that important for the problem of computing n!, however. As we saw in Section 2.1, the function’s values get so large so fast that we can realistically compute exact values of n! only for very small n’s. Again, we use this example just as a simple and convenient vehicle to introduce the standard approach to analyzing recursive algorithms.
Generalizing our experience with investigating the recursive algorithm for computing n!, we can now outline a general plan for investigating recursive algo-rithms.
General Plan for Analyzing the Time Efficiency of Recursive Algorithms
Decide on a parameter (or parameters) indicating an input’s size.
Identify the algorithm’s basic operation.
Check whether the number of times the basic operation is executed can vary on different inputs of the same size; if it can, the worst-case, average-case, and best-case efficiencies must be investigated separately.
Set up a recurrence relation, with an appropriate initial condition, for the number of times the basic operation is executed.
Solve the recurrence or, at least, ascertain the order of growth of its solution.
EXAMPLE 2 As our next example, we consider another educational workhorse of recursive algorithms: the Tower of Hanoi puzzle. In this puzzle, we (or mythical monks, if you do not like to move disks) have n disks of different sizes that can slide onto any of three pegs. Initially, all the disks are on the first peg in order of size, the largest on the bottom and the smallest on top. The goal is to move all the disks to the third peg, using the second one as an auxiliary, if necessary. We can move only one disk at a time, and it is forbidden to place a larger disk on top of a smaller one.
The problem has an elegant recursive solution, which is illustrated in Fig-ure 2.4. To move n > 1 disks from peg 1 to peg 3 (with peg 2 as auxiliary), we first move recursively n − 1 disks from peg 1 to peg 2 (with peg 3 as auxiliary), then move the largest disk directly from peg 1 to peg 3, and, finally, move recursively n −1 disks from peg 2 to peg 3 (using peg 1 as auxiliary). Of course, if n =1, we simply move the single disk directly from the source peg to the destination peg.
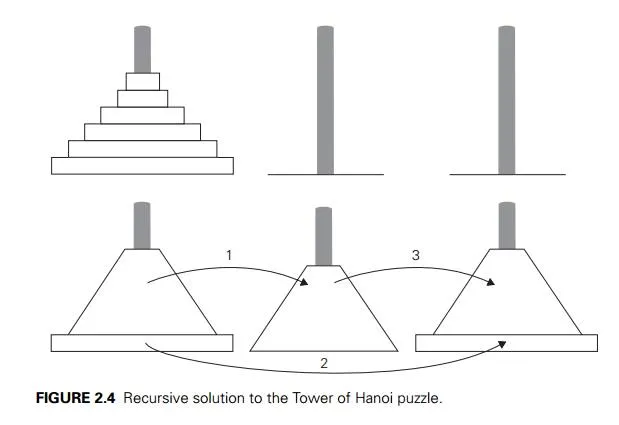
Let us apply the general plan outlined above to the Tower of Hanoi problem. The number of disks n is the obvious choice for the input’s size indicator, and so is moving one disk as the algorithm’s basic operation. Clearly, the number of moves M(n) depends on n only, and we get the following recurrence equation for it:

Thus, we have an exponential algorithm, which will run for an unimaginably long time even for moderate values of n (see Problem 5 in this section’s exercises). This is not due to the fact that this particular algorithm is poor; in fact, it is not difficult to prove that this is the most efficient algorithm possible for this problem. It is the problem’s intrinsic difficulty that makes it so computationally hard. Still, this example makes an important general point:
One should be careful with recursive algorithms because their succinctness may mask their inefficiency.
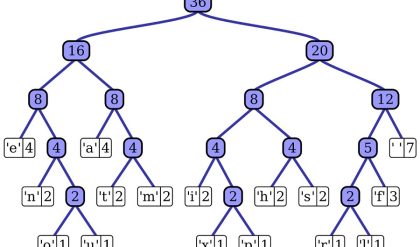
When a recursive algorithm makes more than a single call to itself, it can be useful for analysis purposes to construct a tree of its recursive calls. In this tree, nodes correspond to recursive calls, and we can label them with the value of the parameter (or, more generally, parameters) of the calls. For the Tower of Hanoi example, the tree is given in Figure 2.5. By counting the number of nodes in the tree, we can get the total number of calls made by the Tower of Hanoi algorithm:
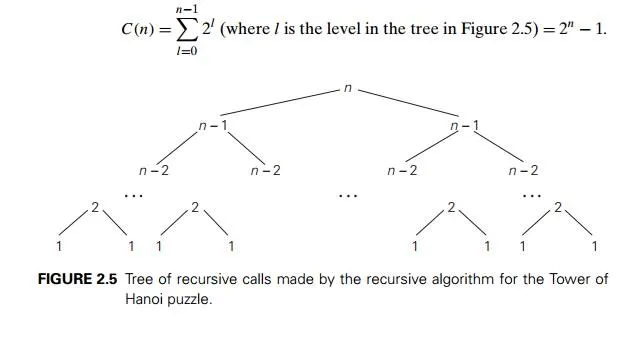
The number agrees, as it should, with the move count obtained earlier.
EXAMPLE 3 As our next example, we investigate a recursive version of the algorithm discussed at the end of Section 2.3.
ALGORITHM BinRec(n)
//Input: A positive decimal integer n
//Output: The number of binary digits in n’s binary representation if n = 1 return 1
else return BinRec( n/2) + 1
Let us set up a recurrence and an initial condition for the number of addi-tions A(n) made by the algorithm. The number of additions made in computing BinRec( n/2) isA( n/2), plus one more addition is made by the algorithm toincrease the returned value by 1. This leads to the recurrence
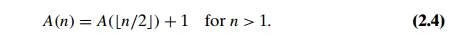
Since the recursive calls end when n is equal to 1 and there are no additions made then, the initial condition is
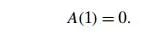
The presence of n/2 in the function’s argument makes the method of back-ward substitutions stumble on values of n that are not powers of 2. Therefore, the standard approach to solving such a recurrence is to solve it only for n = 2k and then take advantage of the theorem called the smoothness rule (see Appendix B), which claims that under very broad assumptions the order of growth observed for n =2k gives a correct answer about the order of growth for all values of n. (Alter-natively, after getting a solution for powers of 2, we can sometimes fine-tune this solution to get a formula valid for an arbitrary n.) So let us apply this recipe to our recurrence, which for n = 2k takes the form

Thus, we end up with
A(2k) = A(1) + k = k,
or, after returning to the original variable n = 2k and hence k = log2 n,
A(n) =log2 n ∈ (log n).
In fact, one can prove (Problem 7 in this section’s exercises) that the exact solution for an arbitrary value of n is given by just a slightly more refined formula A(n) = log2 n
This section provides an introduction to the analysis of recursive algorithms. These techniques will be used throughout the book and expanded further as necessary. In the next section, we discuss the Fibonacci numbers; their analysis involves more difficult recurrence relations to be solved by a method different from backward substitutions.
Exercises 2.4
1. Solve the following recurrence relations.
a. x(n) = x(n − 1) + 5 forn > 1, x(1) =0
b. x(n) = 3x(n − 1) forn > 1, x(1) =4
c. x(n) = x(n − 1) + n forn > 0, x(0) =0
d. x(n) = x(n/2) + n forn > 1, x(1) =1 (solve for n =2k)
e. x(n) = x(n/3) + 1 forn > 1, x(1) =1 (solve for n =3k)
Set up and solve a recurrence relation for the number of calls made by F (n), the recursive algorithm for computing n!.
Consider the following recursive algorithm for computing the sum of the first n cubes: S(n) =13 +23 + . . . + n3.
ALGORITHM S(n)
//Input: A positive integer n
//Output: The sum of the first n cubes if n = 1 return 1
else return S(n − 1) + n ∗ n ∗ n
Set up and solve a recurrence relation for the number of times the algo-rithm’s basic operation is executed.
How does this algorithm compare with the straightforward nonrecursive algorithm for computing this sum?
Consider the following recursive algorithm.
ALGORITHM Q(n)
//Input: A positive integer n if n = 1 return 1
else return Q(n − 1) + 2∗ n − 1
Set up a recurrence relation for this function’s values and solve it to deter-mine what this algorithm computes.
Set up a recurrence relation for the number of multiplications made by this algorithm and solve it.
Set up a recurrence relation for the number of additions/subtractions made by this algorithm and solve it.
Tower of Hanoi
In the original version of the Tower of Hanoi puzzle, as it was published in the 1890s by Edouard Lucas, a French mathematician, the world will end after 64 disks have been moved from a mystical Tower of Brahma. Estimate the number of years it will take if monks could move one disk per minute. (Assume that monks do not eat, sleep, or die.)
How many moves are made by the ith largest disk (1 ≤ i ≤ n) in this algorithm?
Find a nonrecursive algorithm for the Tower of Hanoi puzzle and imple-ment it in the language of your choice.
Restricted Tower of Hanoi Consider the version of the Tower of Hanoi puzzle in which n disks have to be moved from peg A to peg C using peg B so that any move should either place a disk on peg B or move a disk from that peg. (Of course, the prohibition of placing a larger disk on top of a smaller one remains in place, too.) Design a recursive algorithm for this problem and find the number of moves made by it.
a. Prove that the exact number of additions made by the recursive algorithm BinRec(n) for an arbitrary positive decimal integer n is log2 n .
Set up a recurrence relation for the number of additions made by the nonrecursive version of this algorithm (see Section 2.3, Example 4) and solve it.
a. Design a recursive algorithm for computing 2n for any nonnegative integer n that is based on the formula 2n = 2n−1 + 2n−1.
Set up a recurrence relation for the number of additions made by the algorithm and solve it.
Draw a tree of recursive calls for this algorithm and count the number of calls made by the algorithm.
Is it a good algorithm for solving this problem?
Consider the following recursive algorithm.
ALGORITHM Riddle(A[0..n − 1])
//Input: An array A[0..n − 1] of real numbers if n = 1 return A[0]
else temp ← Riddle(A[0..n − 2]) if temp ≤ A[n − 1] return temp else return A[n − 1]
What does this algorithm compute?
Set up a recurrence relation for the algorithm’s basic operation count and solve it.
Consider the following algorithm to check whether a graph defined by its adjacency matrix is complete.
ALGORITHM GraphComplete(A[0..n −1, 0..n −1])
//Input: Adjacency matrix A[0..n − 1, 0..n − 1]) of an undirected graph G //Output: 1 (true) if G is complete and 0 (false) otherwise
if n = 1 return 1 //one-vertex graph is complete by definition
else
if not GraphComplete(A[0..n − 2, 0..n − 2]) return 0 else for j ← 0 to n − 2 do
if A[n − 1, j ]= 0 return 0 return 1
What is the algorithm’s efficiency class in the worst case?
11. The determinant of ann × n matrix
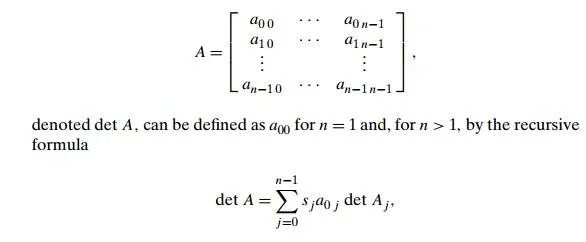
where sj is +1 if j is even and −1 if j is odd, a0 j is the element in row 0 and column j , and Aj is the (n − 1) × (n − 1) matrix obtained from matrix A by deleting its row 0 and column j .
Set up a recurrence relation for the number of multiplications made by the algorithm implementing this recursive definition.
Without solving the recurrence, what can you say about the solution’s order of growth as compared to n!?
12. von Neumann’s neighborhood revisited Find the number of cells in the vonNeumann neighborhood of range n (Problem 12 in Exercises 2.3) by setting up and solving a recurrence relation.
Frying hamburgers There aren hamburgers to be fried on a small grill thatcan hold only two hamburgers at a time. Each hamburger has to be fried on both sides; frying one side of a hamburger takes 1 minute, regardless of whether one or two hamburgers are fried at the same time. Consider the following recursive algorithm for executing this task in the minimum amount of time. If n ≤ 2, fry the hamburger or the two hamburgers together on each side. If n > 2, fry any two hamburgers together on each side and then apply the same procedure recursively to the remaining n − 2 hamburgers.
Set up and solve the recurrence for the amount of time this algorithm needs to fry n hamburgers.
Explain why this algorithm does not fry the hamburgers in the minimum amount of time for all n > 0.
Give a correct recursive algorithm that executes the task in the minimum amount of time.