We are given an array of n points in the plane, and the problem is to find out the closest pair of points in the array. This problem arises in a number of applications. For example, in air-traffic control, you may want to monitor planes that come too close together, since this may indicate a possible collision. Recall the following formula for distance between two points p and q.
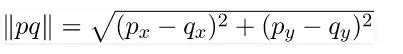
The Brute force solution is O(n^2), compute the distance between each pair and return the smallest. We can calculate the smallest distance in O(nLogn) time using Divide and Conquer strategy. In this post, a O(n x (Logn)^2) approach is discussed. We will be discussing a O(nLogn) approach in a separate post.
Algorithm
Following are the detailed steps of a O(n (Logn)^2) algortihm.
Input: An array of n points P[]
Output: The smallest distance between two points in the given array.
As a pre-processing step, the input array is sorted according to x coordinates.
1) Find the middle point in the sorted array, we can take P[n/2] as middle point.
2) Divide the given array in two halves. The first subarray contains points from P[0] to P[n/2]. The second subarray contains points from P[n/2+1] to P[n-1].
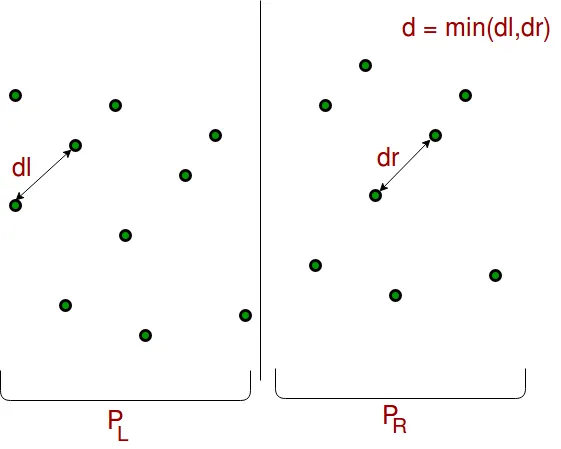
3) Recursively find the smallest distances in both subarrays. Let the distances be dl and dr. Find the minimum of dl and dr. Let the minimum be d.
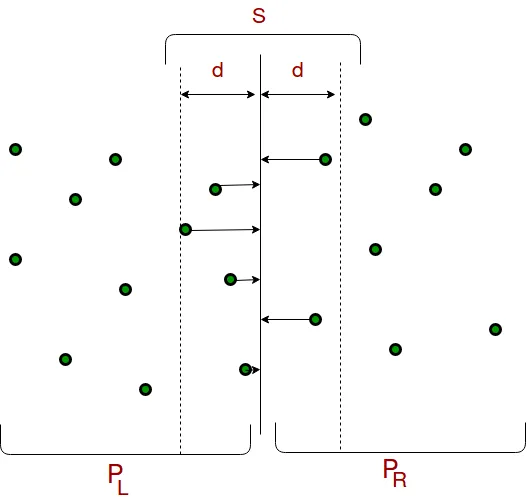
4) From the above 3 steps, we have an upper bound d of minimum distance. Now we need to consider the pairs such that one point in pair is from the left half and the other is from the right half. Consider the vertical line passing through P[n/2] and find all points whose x coordinate is closer than d to the middle vertical line. Build an array strip[] of all such points.
5) Sort the array strip[] according to y coordinates. This step is O(nLogn). It can be optimized to O(n) by recursively sorting and merging.
6) Find the smallest distance in strip[]. This is tricky. From the first look, it seems to be a O(n^2) step, but it is actually O(n). It can be proved geometrically that for every point in the strip, we only need to check at most 7 points after it (note that strip is sorted according to Y coordinate). See this for more analysis.
7) Finally return the minimum of d and distance calculated in the above step (step 6)
Implementation
Following is C/C++ implementation of the above algorithm.
· C++
· C
filter_none
edit
play_arrow
brightness_4
| // A divide and conquer program in C++ // to find the smallest distance from a // given set of points. #include <bits/stdc++.h>using namespace std; // A structure to represent a Point in 2D plane class Point { public: int x, y; }; /* Following two functions are needed for library function qsort(). // Needed to sort array of points // according to X coordinate int compareX(const void* a, const void* b) { Point *p1 = (Point *)a, *p2 = (Point *)b; return (p1->x – p2->x); } // Needed to sort array of points according to Y coordinate int compareY(const void* a, const void* b) { Point *p1 = (Point *)a, *p2 = (Point *)b; return (p1->y – p2->y); } // A utility function to find the // distance between two points float dist(Point p1, Point p2) { return sqrt( (p1.x – p2.x)*(p1.x – p2.x) + (p1.y – p2.y)*(p1.y – p2.y) ); } // A Brute Force method to return the // smallest distance between two points // in P[] of size n float bruteForce(Point P[], int n) { float min = FLT_MAX; for (int i = 0; i < n; ++i) for (int j = i+1; j < n; ++j) if (dist(P[i], P[j]) < min) min = dist(P[i], P[j]); return min; } // A utility function to find // minimum of two float values float min(float x, float y) { return (x < y)? x : y; } // A utility function to find the // distance beween the closest points of // strip of given size. All points in // strip[] are sorted accordint to // y coordinate. They all have an upper// bound on minimum distance as d. // Note that this method seems to be // a O(n^2) method, but it’s a O(n) // method as the inner loop runs at most 6 times float stripClosest(Point strip[], int size, float d) { float min = d; // Initialize the minimum distance as d qsort(strip, size, sizeof(Point), compareY); // Pick all points one by one and try the next points till the difference // between y coordinates is smaller than d. // This is a proven fact that this loop runs at most 6 times for (int i = 0; i < size; ++i) for (int j = i+1; j < size && (strip[j].y – strip[i].y) < min; ++j) if (dist(strip[i],strip[j]) < min) min = dist(strip[i], strip[j]); return min; } // A recursive function to find the // smallest distance. The array P contains // all points sorted according to x coordinate float closestUtil(Point P[], int n) { // If there are 2 or 3 points, then use brute force if (n <= 3) return bruteForce(P, n); // Find the middle point int mid = n/2; Point midPoint = P[mid]; // Consider the vertical line passing // through the middle point calculate // the smallest distance dl on left // of middle point and dr on right side float dl = closestUtil(P, mid); float dr = closestUtil(P + mid, n – mid); // Find the smaller of two distances float d = min(dl, dr); // Build an array strip[] that contains // points close (closer than d) // to the line passing through the middle point Point strip[n]; int j = 0; for (int i = 0; i < n; i++) if (abs(P[i].x – midPoint.x) < d) strip[j] = P[i], j++; // Find the closest points in strip. // Return the minimum of d and closest // distance is strip[] return min(d, stripClosest(strip, j, d) ); } // The main function that finds the smallest distance // This method mainly uses closestUtil() float closest(Point P[], int n) { qsort(P, n, sizeof(Point), compareX); // Use recursive function closestUtil() // to find the smallest distance return closestUtil(P, n); } // Driver code int main() { Point P[] = {{2, 3}, {12, 30}, {40, 50}, {5, 1}, {12, 10}, {3, 4}}; int n = sizeof(P) / sizeof(P[0]); cout << “The smallest distance is ” << closest(P, n); return 0; } // This is code is contributed by rathbhupendra |
Output:
The smallest distance is 1.414214
Time Complexity Let Time complexity of above algorithm be T(n). Let us assume that we use a O(nLogn) sorting algorithm. The above algorithm divides all points in two sets and recursively calls for two sets. After dividing, it finds the strip in O(n) time, sorts the strip in O(nLogn) time and finally finds the closest points in strip in O(n) time. So T(n) can expressed as follows
T(n) = 2T(n/2) + O(n) + O(nLogn) + O(n)
T(n) = 2T(n/2) + O(nLogn)
T(n) = T(n x Logn x Logn)


