Whether it is possible to traverse a graph from one vertex to another is determined by how a graph is connected. Connectivity is a basic concept in Graph Theory. Connectivity defines whether a graph is connected or disconnected.

Connectivity

A graph is said to be connected if there is a path between every pair of vertex. From every vertex to any other vertex, there should be some path to traverse. That is called the connectivity of a graph. A graph with multiple disconnected vertices and edges is said to be disconnected.

Cut Vertex

Let ‘G’ be a connected graph. A vertex V ∈ G is called a cut vertex of ‘G’, if ‘G-V’ (Delete ‘V’ from ‘G’) results in a disconnected graph. Removing a cut vertex from a graph breaks it in to two or more graphs.

Note − Removing a cut vertex may render a graph disconnected.

A connected graph ‘G’ may have at most (n–2) cut vertices.

Example

In the following graph, vertices ‘e’ and ‘c’ are the cut vertices.

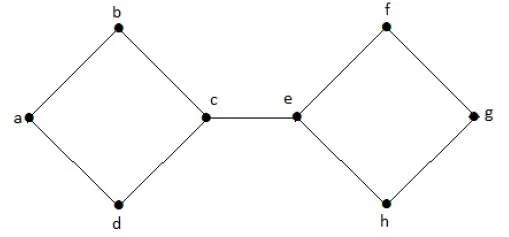
By removing ‘e’ or ‘c’, the graph will become a disconnected graph.

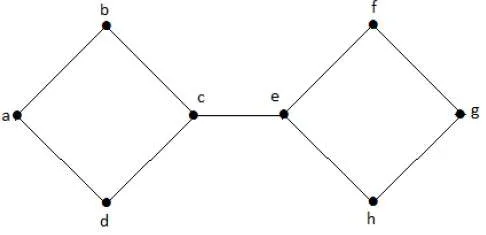
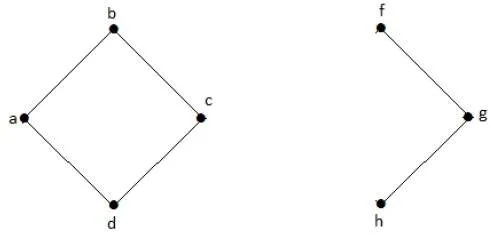
Without ‘g’, there is no path between vertex ‘c’ and vertex ‘h’ and many other. Hence it is a disconnected graph with cut vertex as ‘e’. Similarly, ‘c’ is also a cut vertex for the above graph.

Cut Edge (Bridge)

Let ‘G’ be a connected graph. An edge ‘e’ ∈ G is called a cut edge if ‘G-e’ results in a disconnected graph.

If removing an edge in a graph results in to two or more graphs, then that edge is called a Cut Edge.

Example

In the following graph, the cut edge is [(c, e)]

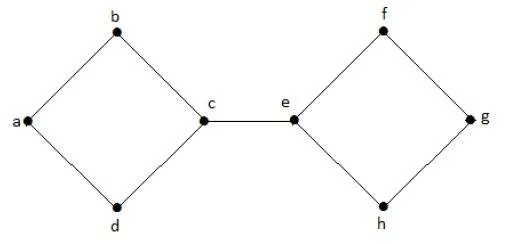
By removing the edge (c, e) from the graph, it becomes a disconnected graph.

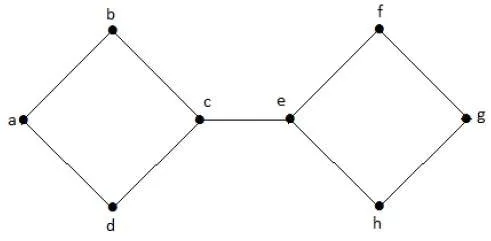
In the above graph, removing the edge (c, e) breaks the graph into two which is nothing but a disconnected graph. Hence, the edge (c, e) is a cut edge of the graph.

Note − Let ‘G’ be a connected graph with ‘n’ vertices, then

·         a cut edge e ∈ G if and only if the edge ‘e’ is not a part of any cycle in G.

·         the maximum number of cut edges possible is ‘n-1’.

·         whenever cut edges exist, cut vertices also exist because at least one vertex of a cut edge is a cut vertex.

·         if a cut vertex exists, then a cut edge may or may not exist.

Cut Set of a Graph

Let ‘G’= (V, E) be a connected graph. A subset E’ of E is called a cut set of G if deletion of all the edges of E’ from G makes G disconnect.

If deleting a certain number of edges from a graph makes it disconnected, then those deleted edges are called the cut set of the graph.

Example

Take a look at the following graph. Its cut set is E1 = {e1, e3, e5, e8}.

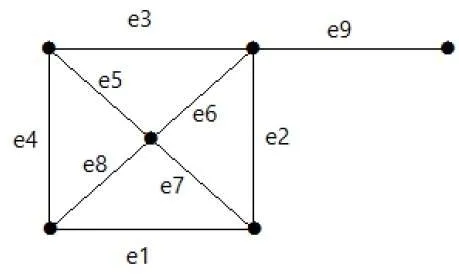
After removing the cut set E1 from the graph, it would appear as follows −

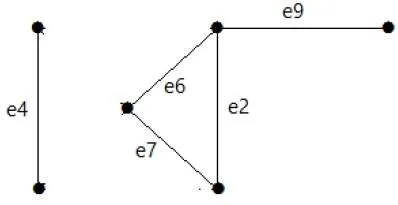
Similarly there are other cut sets that can disconnect the graph −

• E3 = {e9} – Smallest cut set of the graph.
• E4 = {e3, e4, e5}