An Euler graph may be defined as-

Euler Graph Example-

The following graph is an example of an Euler graph-

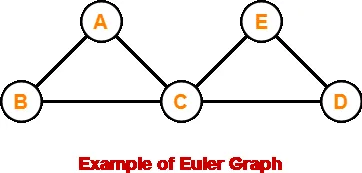
Here,

·         This graph is a connected graph and all its vertices are of even degree.

·         Therefore, it is an Euler graph.

Alternatively, the above graph contains an Euler circuit BACEDCB, so it is an Euler graph.

Also Read- Planar Graph

Euler Path-

Euler path is also known as Euler Trail or Euler Walk.

·         If there exists a Trail in the connected graph that contains all the edges of the graph, then that trail is called as an Euler trail.

OR

·         If there exists a walk in the connected graph that visits every edge of the graph exactly once with or without repeating the vertices, then such a walk is called as an Euler walk.

NOTEA graph will contain an Euler path if and only if it contains at most two vertices of odd degree.

Euler Path Examples-

Examples of Euler path are as follows-

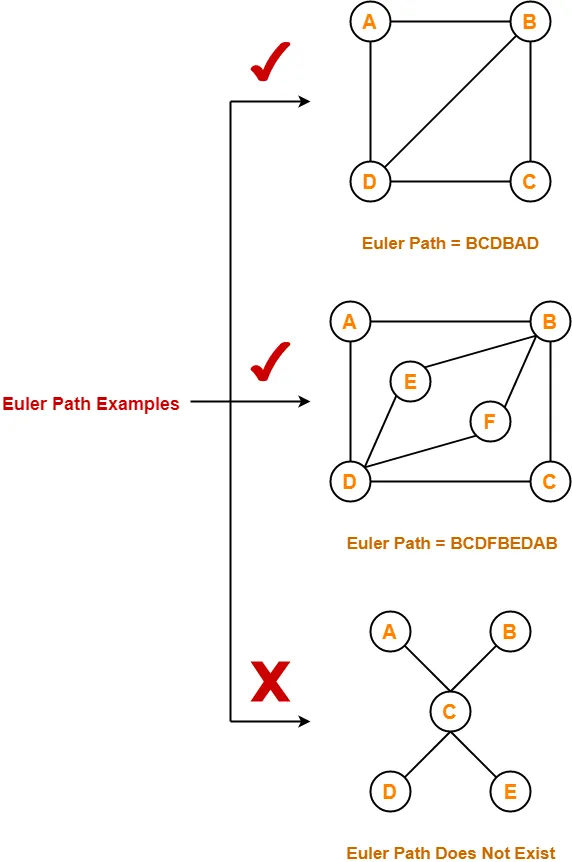
Euler Circuit-

Euler circuit is also known as Euler Cycle or Euler Tour.

·         If there exists a Circuit in the connected graph that contains all the edges of the graph, then that circuit is called as an Euler circuit.

OR

·         If there exists a walk in the connected graph that starts and ends at the same vertex and visits every edge of the graph exactly once with or without repeating the vertices, then such a walk is called as an Euler circuit.

OR

·         An Euler trail that starts and ends at the same vertex is called as an Euler circuit.

OR

·         A closed Euler trail is called as an Euler circuit.

NOTEA graph will contain an Euler circuit if and only if all its vertices are of even degree.

Euler Circuit Examples-

Examples of Euler circuit are as follows-

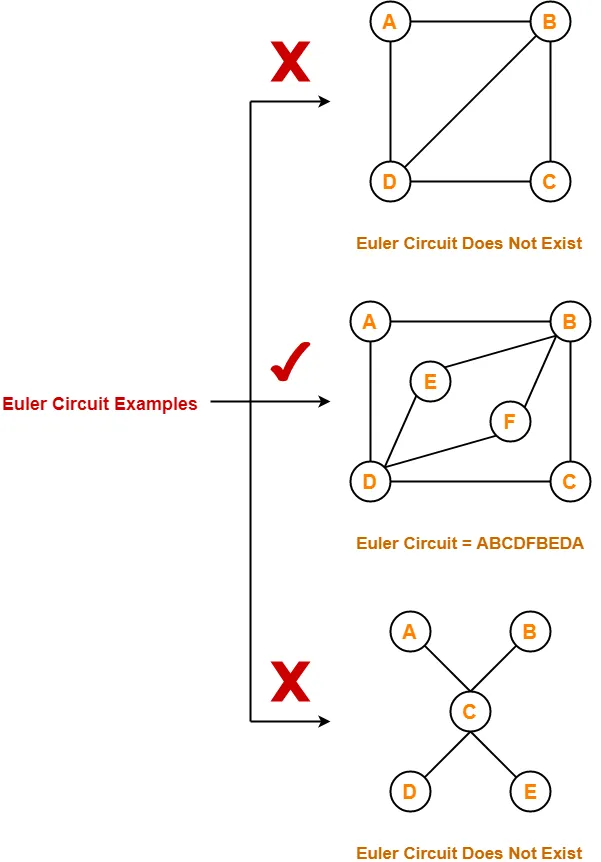
Semi-Euler Graph-

If a connected graph contains an Euler trail but does not contain an Euler circuit, then such a graph is called as a semi-Euler graph.

Thus, for a graph to be a semi-Euler graph, following two conditions must be satisfied-

·         Graph must be connected.

·         Graph must contain an Euler trail.

Example-

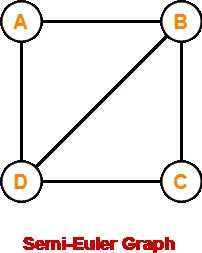
Here,

·         This graph contains an Euler trail BCDBAD.

·         But it does not contain an Euler circuit.

·         Therefore, it is a semi-Euler graph.