Problem Statement

Let X = (Q_x, ∑, δ_x, q₀, F_x) be an NDFA which accepts the language L(X). We have to design an equivalent DFA Y = (Q_y, ∑, δ_y, q₀, F_y) such that L(Y) = L(X). The following procedure converts the NDFA to its equivalent DFA −

Algorithm

Input − An NDFA

Output − An equivalent DFA

Step 1 − Create state table from the given NDFA.

Step 2 − Create a blank state table under possible input alphabets for the equivalent DFA.

Step 3 − Mark the start state of the DFA by q0 (Same as the NDFA).

Step 4 − Find out the combination of States {Q₀, Q₁,… , Q_n} for each possible input alphabet.

Step 5 − Each time we generate a new DFA state under the input alphabet columns, we have to apply step 4 again, otherwise go to step 6.

Step 6 − The states which contain any of the final states of the NDFA are the final states of the equivalent DFA.

Example

Let us consider the NDFA shown in the figure below.

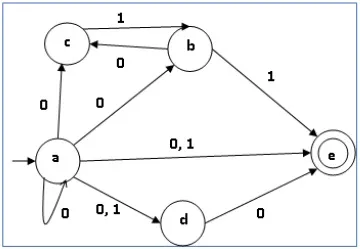
q	δ(q,0)	δ(q,1)
a	{a,b,c,d,e}	{d,e}
b	{c}	{e}
c	∅	{b}
d	{e}	∅
e	∅	∅

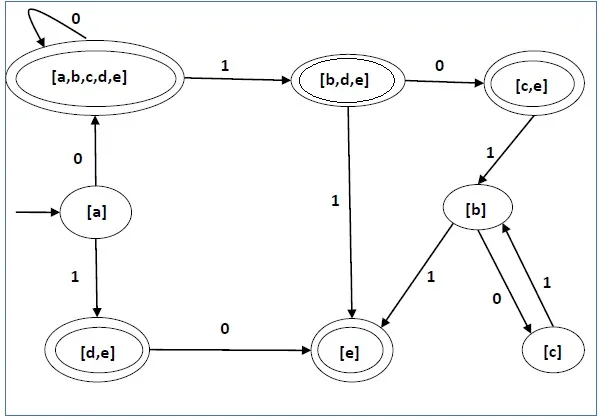
Using the above algorithm, we find its equivalent DFA. The state table of the DFA is shown in below.

q	δ(q,0)	δ(q,1)
[a]	[a,b,c,d,e]	[d,e]
[a,b,c,d,e]	[a,b,c,d,e]	[b,d,e]
[d,e]	[e]	∅
[b,d,e]	[c,e]	[e]
[e]	∅	∅
[c, e]	∅	[b]
[b]	[c]	[e]
[c]	∅	[b]

The state diagram of the DFA is as follows −