DFA Minimization using Myphill-Nerode Theorem

Algorithm

Input − DFA

Output − Minimized DFA

Step 1 − Draw a table for all pairs of states (Q_i, Q_j) not necessarily connected directly [All are unmarked initially]

Step 2 − Consider every state pair (Q_i, Q_j) in the DFA where Q_i ∈ F and Q_j ∉ F or vice versa and mark them. [Here F is the set of final states]

Step 3 − Repeat this step until we cannot mark anymore states −

If there is an unmarked pair (Q_i, Q_j), mark it if the pair {δ (Q_i, A), δ (Q_i, A)} is marked for some input alphabet.

Step 4 − Combine all the unmarked pair (Q_i, Q_j) and make them a single state in the reduced DFA.

Example

Let us use Algorithm 2 to minimize the DFA shown below.

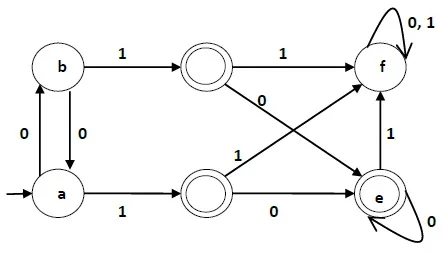
Step 1 − We draw a table for all pair of states.

	a	b	c	d	e	f
a
b
c
d
e
f

Step 2 − We mark the state pairs.

	a	b	c	d	e	f
a
b
c	✔	✔
d	✔	✔
e	✔	✔
f			✔	✔	✔

Step 3 − We will try to mark the state pairs, with green colored check mark, transitively. If we input 1 to state ‘a’ and ‘f’, it will go to state ‘c’ and ‘f’ respectively. (c, f) is already marked, hence we will mark pair (a, f). Now, we input 1 to state ‘b’ and ‘f’; it will go to state ‘d’ and ‘f’ respectively. (d, f) is already marked, hence we will mark pair (b, f).

	a	b	c	d	e	f
a
b
c	✔	✔
d	✔	✔
e	✔	✔
f	✔	✔	✔	✔	✔

After step 3, we have got state combinations {a, b} {c, d} {c, e} {d, e} that are unmarked.

We can recombine {c, d} {c, e} {d, e} into {c, d, e}

Hence we got two combined states as − {a, b} and {c, d, e}

So the final minimized DFA will contain three states {f}, {a, b} and {c, d, e}

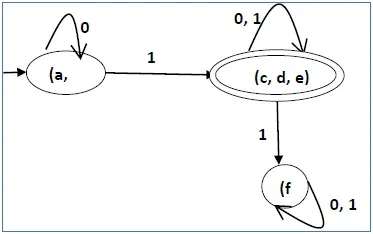
DFA Minimization using Equivalence Theorem

If X and Y are two states in a DFA, we can combine these two states into {X, Y} if they are not distinguishable. Two states are distinguishable, if there is at least one string S, such that one of δ (X, S) and δ (Y, S) is accepting and another is not accepting. Hence, a DFA is minimal if and only if all the states are distinguishable.

Algorithm 3

Step 1 − All the states Q are divided in two partitions − final states and non-final states and are denoted by P₀. All the states in a partition are 0^th equivalent. Take a counter k and initialize it with 0.

Step 2 − Increment k by 1. For each partition in P_k, divide the states in P_k into two partitions if they are k-distinguishable. Two states within this partition X and Y are k-distinguishable if there is an input S such that δ(X, S) and δ(Y, S) are (k-1)-distinguishable.

Step 3 − If P_k ≠ P_k-1, repeat Step 2, otherwise go to Step 4.

Step 4 − Combine k^th equivalent sets and make them the new states of the reduced DFA.

Example

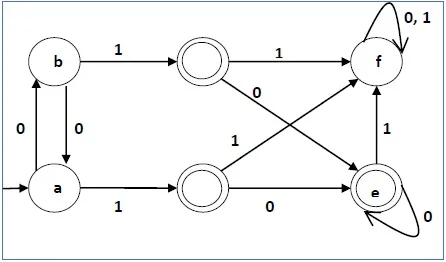
Let us consider the following DFA −

q	δ(q,0)	δ(q,1)
a	b	c
b	a	d
c	e	f
d	e	f
e	e	f
f	f	f

Let us apply the above algorithm to the above DFA −

• P₀ = {(c,d,e), (a,b,f)}
• P₁ = {(c,d,e), (a,b),(f)}
• P₂ = {(c,d,e), (a,b),(f)}

Hence, P₁ = P₂.

There are three states in the reduced DFA. The reduced DFA is as follows −

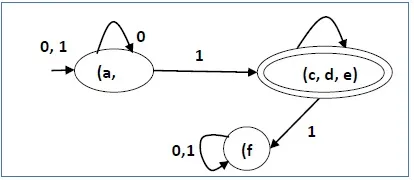
Q	δ(q,0)	δ(q,1)
(a, b)	(a, b)	(c,d,e)
(c,d,e)	(c,d,e)	(f)
(f)	(f)	(f)